Perpendicular slope calculator
Instructions: Use this graphing tool to plot the find, step-by-step, the slope of a perpendicular line to a line that has a given slope. Please provide the slope of your line (any valid numeric expression).
More about this perpendicular slope calculator.
Often times we need to deal with lines and other lines that are perpendicular to them. Perpendicularity has to do with having a 90o angle between the lines.
But the question is, how do we relate this perpendicularity of two lines with the slopes of the two lines?
The answer is simple: two lines with slopes \(m_1\) and \(m_2\) are perpendicular if and only if
\[m_1 \cdot m_2 = -1\]
How do you compute the perpendicular slope?
The answer is right there. If you know \(m_1\), then all you need to do is to solve the slope for the line that is perpendicular, \(m_2\), so we get the following formula for the perpendicular slope:
\[\displaystyle m_2 = -\frac{1}{m_1}\]which is the formula for the perpendicular slope from the slope of the line.
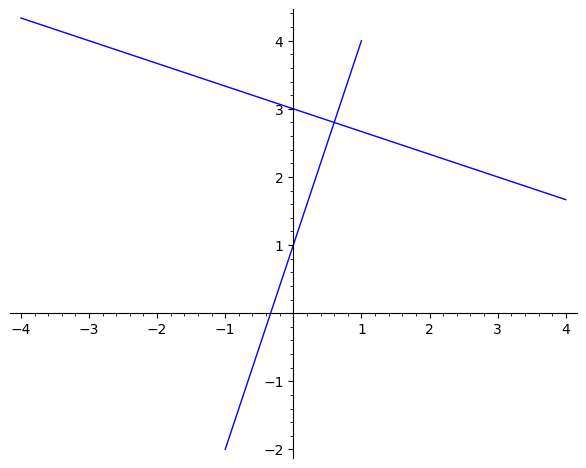
How do you compute the perpendicular slope if you have the equation of a line?
In that case, the first you need to do is to convert the equation into slope-intercept form. Once you know the slope, you will be able to use the formula presented above.
Ultimately, once you have the slope of the perpendicular line, by knowing one point of that perpendicular line passes through, you can actually compute the equation of the perpendicular line.
Example: Calculation of the slope of a perpendicular line
Consider the line with equation \(x + 3y = 2)\). Find the slope of the perpendicular line to the given line.
Solution: The equation can be rewritten as: \[3y = -x + 2\] \[\Rightarrow y = \displaystyle -\frac{1}{3} x + \frac{2}{3}\] Hence, the given slope of the line provided is \(m = \displaystyle -\frac{ 1}{ 3}\), and we need to compute the perpendicular slope.
The formula needed to compute the perpendicular slope, \(m_{\perp}\), is:
\[m_{\perp} = \displaystyle -\frac{1}{m}\]By plugging the value of \(m = -\frac{ 1}{ 3}\) in the formula, we find that the perpendicular slope is
\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{-\frac{ 1}{ 3}} = 3\]Therefore, we conclude that the perpendicular slope is \(m_{\perp} = 3 \)
