Log Rules
The logarithmic function is one of the most important functions in Math, and the log rules are simple and convenient, making it really easy to work with logarithms.
Let us first recall what is the meaning of \(\log_b a\). In this context, the value \(b\) is the base of the logarithm, and \(a\) is the argument .
We say that \(\log_b a = y\) when \(b^y = a\). This is saying that \(\log_b a\) is the number that \(b\) (the base) needs to be raised to in order to get \(a\) (the argument).
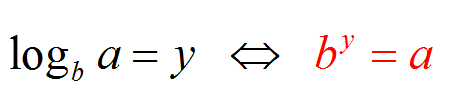
For example, \(\log_{10} 25\) corresponds to the number that I need to raise 10 to, in order to get 25. So logarithm I am looking for is the number \(y\) that has the property that \(10^y = 25\)
Now the question is, how we compute that number \(y\) that has the property \(10^y = 25\)? Well, that number is well defined, and the logarithmic function \(f(x) = \log_{10} x\) takes care of it. This function is not an elementary function, and a Taylor Series (infinite series) is needed to represent it.
Or, you can use a calculator (which is probably easier, right?).
The Log-Rules: Properties of Logarithms
These are main log-rules:
Rule #1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Rule #2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Rule #3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Rule #4 : \(\large \log_a (a) = 1 \)
Rule #5 : \(\large \log_a (1) = 0 \)
EXAMPLE 1
Simplify \(\log_2 8 + \log_2 4\) using Log Rules:
ANSWER:
Using Rule #1, we find that:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]So, the first step is a simple application of Rule #1, but how do we get that \(\log_2 32 = 5\)? It is because \(2^5 = 32\), so in this case we find directly what is the number you need to raise \(2\) in order to get \(32\).
Majority of logarithms you will need a calculator to compute them. It is only a selected few that you can compute directly. Stuff like \(\log_{10} 100 = 2\), because you know easily that \(10^2 = 100\).
But, can you compute \(\log_{10} 102\) directly? Not really, you need a calculator for that.
EXAMPLE 2
Express a the sum and subtraction of logarithms: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
ANSWER:
First of all, we need to remember that taking a cubic root is the as raising to the \(1/3\) power. In other words, \(\sqrt[3]{x}\) is the same as \(x^{1/3}\).
So then, we first use Rule #3 to bring the power in front of the logarithm, and then we use Rules #1 and #2. We get:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]which is what was required: sum and subtractions of simple logarithms.
The Change of Base Formula for Logarithms
One of the most useful formulas relating to logarithms is the change of base formula. This formula goes like this:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]This formula is just saying that if you want to change the base from \(b\) to \(c\), the results is essentially the same, but you need to divide by the logarithm of the new base.
Now, if you are artistically oriented, you may enjoy the alternative form of the change of based formula expressed below:
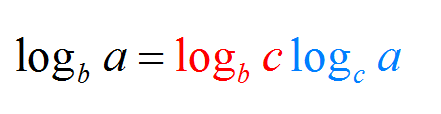
EXAMPLE 3
Express the natural log \(\ln\) in terms of \(\log\) (base 10).
ANSWER:
Using the change of base formula, we get that:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]So you are saying the \(\ln a\) is obtained by dividing \(\log a\) by \(\log e\). How convenient? Who says Math was hard, huh?
More About the Log-Rules
Logarithms are really important in Math. Historically, logarithms play a very important role in Astronomy, as a way of predicting the movement of the moon and planets.
The logarithmic functions lies in the middle of everything in Math, it intertwines with exponential, exponents and pretty much everything. That is why they ask you to learn logarithms by heart, because they are important.
Also, these log rules presented here play a crucial role at facilitating the resolution of logarithmic equations .
Notation Conventions
There are a couple of notation conventions you need to know about. In general, we write \(\log_b a\), and we say it "log base b of a". When the base is \(b = 10\), by convention we just write \(\log a\). So when you see a \(\log\) without a base, it is assumed that the base is \(10\).
There is another notable case. For \(\log_b a\), when the base is \(b = e\) (the Euler constant), then we write \(\ln a\) instead of \(\log_e a\). So, when \(\ln\) is used instead of \(\log\), it is because the base of the logarithm is \(e\).
Observe that \(\ln a\) is usually referred as the natural log . And yes, natural logs have the same rules as the general log.
If you have a logarithmic function that you would like to graph, you can try our Logarithmic Function Graph maker , which will provide you with a neatly presented graph.
