Midpoint Formula Calculator

This calculator will allow you to find the midpoint between two points. All you have to do is to provide the coordinates of the two points, and then click on "Calculate" to get all the steps shown.

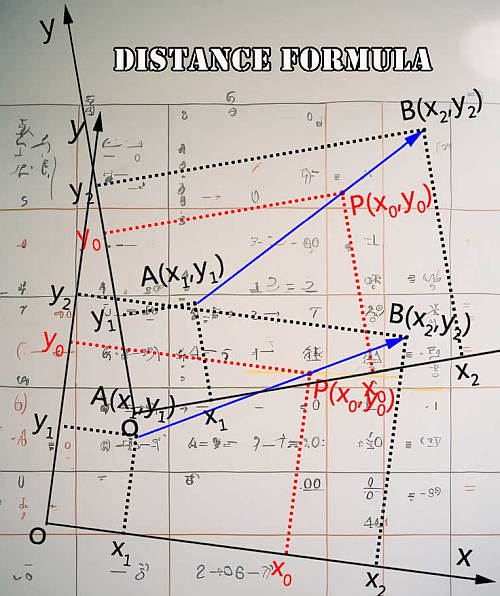
First of all, we need to recall that the distance between two points in the Euclidean plane is based on the concept of the basic geometric principles that allow use to use the Pythagorean theorem.

How do you calculate midpoint?

Conceptually speaking, the midpoint is the point that is half-way between the two points. This idea of half-way is in line with the geometric theorems of proportionality.

The midpoint is an ordered pair that is half-way between two given points. That is the first thing you need to know: some people mistakenly think of one quantity as the midpoint, and actually what you are looking at getting is an ordered pair.

The midpoint for the given points \((x_1, y_1)\) and \((x_2, y_2)\) is given by the following formula:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]

Explanation of the midpoint formula

Formula Definition: The above midpoint formula is tightly related with the distance formula. Indeed, what the above formula does is very simply that it takes the average of the two corresponding coordinates.

This is, the first coordinate of the midpoint is the average of the first coordinates of the two given points, and the second coordinate of the midpoint is the average of the second coordinates of the two given points. How to use the above formula? Please check out the examples below.

What do I use the midpoint formula for?

The idea of midpoint is so familiar with us because it is tightly associated to the idea of "half way" from one point to the another. Such situations are very common in real life, where we may be interested in dividing something, for example.

Naturally, the process of dividing something does not have to necessarily involve a midpoint, but usually when doing an equal division, it will.

So then, the midpoint formula is so useful in part because it is a way of using the distance formula in a very special case, where the point we are finding is a the same distance from both of the points given.

Midpoint formula examples

Assume that we have two points \((1, 3)\) and \((4, 8)\), then the midpoint formula is computed as follows:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) = \left( \frac{1 + 4}{2}, \frac{3+ 8}{2} \right) = \left( \frac{5}{2}, \frac{11}{2} \right) \]

Sometimes you leave the answer as a fraction, or sometimes you are instructed to compute the answer with decimals, in which case the midpoint would be (2.5, 5.5) in the previous example.

More Midpoint Examples

How to deal with midpoint formula with fractions? It is the same procedure. Assume that we have two points \((\frac{1}{2}, \frac{1}{4})\) and \((\frac{3}{5}, \frac{3}{4})\), then the midpoint is computed as:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = \left( \frac{1/2 + 3/5}{2}, \frac{1/4+ 3/4}{2} \right) = \left( \frac{11/10}{2}, \frac{1}{2} \right) = \left( \frac{11}{20}, \frac{1}{2} \right) \]

Does this have to do anything with Pythagoras

Almost everything has to do with Pythagoras. The midpoint of the hypotenuse will project to the midpoint of the legs for a right triangle. Also, you can take the two points, and you can compute the distance between them , using Pythagorean formula.