Solvers Calculus

Quotient Rule

Instructions: Use this Quotient Rule calculator to find the derivative of function involving quotients that you provide , showing all the steps. Please type the function in the form box below.

The Quotient Rule

This calculator will allow you to use the Quotient Rule for a function that involves a quotient, showing all the steps of the process. All you need to provide is a valid differentiable function. This function needs to involve at least one quotient in order for the quotient rule to be applicable.

An example of a valid function would be f(x) = (x^2 + 2x + 1)/(x^2-1), or something like f(x) = sin(x)/x, etc.

Once a valid function involving quotients is provided, you have to click on the "Calculate" button to get the steps of the calculation shown.

Along with the product rule and chain rule, the quotient rule is one of the most important basic derivative rules.

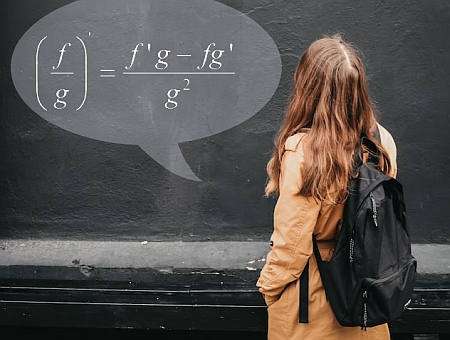
Quotient Rule Formula

In simple terms, the quotient rule helps you to compute the derivative of a quotient, using the knowledge of the individual functions and their derivatives. The quotient rule formula is:

\[\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \]

What are the steps for using the Quotient Rule?

Step 1: Identify clearly the functions f(x) and g(x) that go in the numerator and denominator of the quotient
Step 2: Simplify any obvious term that can be simplified
Step 3: Calculate the corresponding derivatives f'(x) and g'(x)
Step 4: Plug the values found in Step 3 in the formula \(\displaystyle \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \displaystyle \frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)} \)

Notice that f(x) and g(x) may still be complex functions, so you may need to use other rules like the chain rule to compute both f'(x) and g'(x).

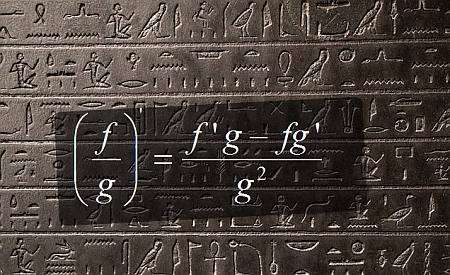
Quotient rule derivative

When computing a quotient rule derivative, you are reducing the derivative of a quotient to the knowledge of the individual derivatives, but those individual derivatives may still require many steps with basic derivative rules to be solved.

That is why differentiation is considered a 'straightforward' operation, but still, you need to sufficiently organized and keep track of all the pieces that arise when decomposing with derivative rules, and then proceed with the smaller pieces that may require more differentiation rules to be applied.

So you may end up with an iterative process, but it is guaranteed to end at some point by going deeper into each smaller part, until you find an elementary derivative, such a polynomial or a trig derivative.

Quotient rule in differentiation

The role of the quotient rule in differentiation is pretty important, a good reason why you will want to use a calculator for it. In algebraic terms, the quotient rule could be considered to be more convoluted than the product rule, and it could be true in many case, but yet it ultimately depends on the complexity of the functions in the numerator and denominator.

Quotient Rule Examples

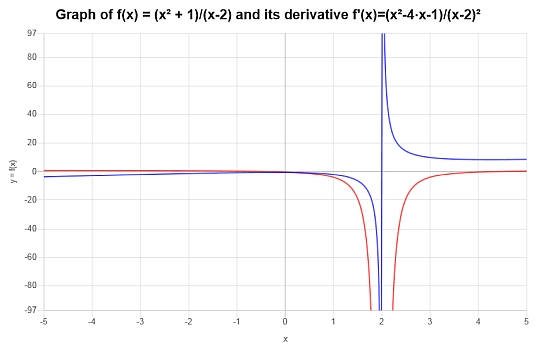
Consider the function: \(f(x) = \frac{x^2+1}{x-2}\), find its derivative.

Solution: For this example, we need to analyze the function \(\displaystyle f(x)=\frac{x^2+1}{x-2}\), in terms of finding its derivative.

\( \displaystyle \frac{d}{dx}\left(\frac{x^2+1}{x-2}\right)\)

By using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x^2+1}{x-2} \right) = \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \cdot \frac{d}{dx}\left(x^2+1\right)-\left(x^2+1 \right) \cdot \frac{d}{dx}\left(x-2\right)}{\left(x-2\right)^2}\)

By linearity, we know \(\frac{d}{dx}\left( x-2 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\) and \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(2\right)\right)}{\left(x-2\right)^2}\)

Since the derivative of a constant is 0, we get that:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right) \left(\frac{d}{dx}\left(x\right)\right)}{\left(x-2\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(\frac{d}{dx}\left(x^2\right)\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

In this case we use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x-2\right) \left(2x\right)-\left(x^2+1 \right)}{\left(x-2\right)^2}\)

and then we get

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x\left(x-2\right)-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Note that \((2x) \cdot (x-2) = 2x^2-2\cdot 2x = 2x^2-4x\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-\left(x^2+1\right)}{\left(x-2\right)^2}\)

Removing unnecessary parentheses and multiplying the terms by \(-1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2x^2-4x-x^2-1}{\left(x-2\right)^2}\)

Aggregating those terms with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+\left(-1+2\right)x^2-1}{\left(x-2\right)^2}\)

Putting together the numerical values and operating the terms that were grouped with \(x^2\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-4x+x^2-1}{\left(x-2\right)^2}\)

Conclusion: We find that the derivative of the given function is:

\[f'(x) = \frac{x^2-4x-1}{\left(x-2\right)^2}\]

So then, the graphical depiction of the function and its derivative is \([-5, 5]\):

Example: Quotient Rule Calculation

Now consider \(f(x) = \frac{x}{\sin(x)}\), find its derivative using the Quotient Rule.

Solution: For this second example, the function we are interested in is \(\displaystyle f(x)=\frac{x}{\sin\left(x\right)}\). Let's differentiate it using the Quotient Rule.

\( \displaystyle \frac{d}{dx}\left(\frac{x}{\sin\left(x\right)}\right)\)

Using the Quotient Rule: \(\frac{d}{dx}\left( \frac{x}{\sin\left(x\right)} \right) = \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) \cdot \frac{d}{dx}\left(x\right)-x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

We already know that \(\frac{d}{dx}\left(x\right) = 1\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \frac{d}{dx}\left(\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

Directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right) -x\cdot \cos\left(x\right)}{\sin\left(x\right)^2}\)

so then we get that

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\sin\left(x\right)-x\cos\left(x\right)}{\sin\left(x\right)^2}\)

By reorganizing/simplifying/expanding the terms that are amenable to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\)

Conclusion: The conclusion is that, based on the above calculation, the derivative is given by:

\[f'(x) = \frac{-\left(x\cos\left(x\right)-\sin\left(x\right)\right)}{\sin\left(x\right)^2}\]

Graphically, we can see the function (in blue) and its derivative (in red):

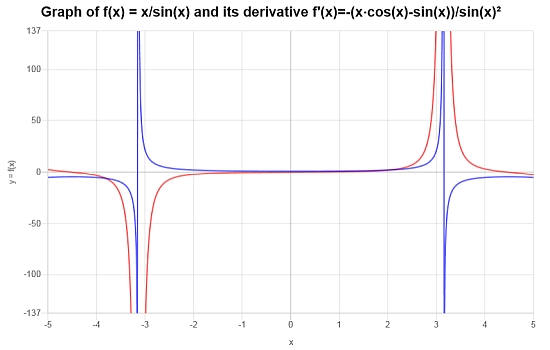
More Quotient Rule Examples

Finally, consider the function: \(f(x) = \frac{\sin(x)}{x^2}\), find its derivative.

Solution: For this final quotient rule example we work with the function \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x^2}\). .

\( \displaystyle \frac{d}{dx}\left(\frac{\sin\left(x\right)}{x^2}\right)\)

The Quotient Rule applies: \(\frac{d}{dx}\left( \frac{\sin\left(x\right)}{x^2} \right) = \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)-\sin\left(x\right)\cdot \frac{d}{dx}\left(x^2\right)}{\left(x^2\right)^2}\)

We use the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and directly differentiating: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\left(x^2\right) \cdot \cos\left(x\right)-\sin\left(x\right)\cdot 2x}{\left(x^2\right)^2}\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \frac{\cos\left(x\right)\cdot x^2-\sin\left(x\right)\cdot 2x}{x^4}\)

By simplifying and regrouping terms

\( \displaystyle = \,\,\)

\(\displaystyle \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\)

Conclusion: For the given function, its derivative is:

\[f'(x) = \frac{x\cos\left(x\right)-2\sin\left(x\right)}{x^3}\]

The graph below depicts the situation for \(f\) and \(f'\):

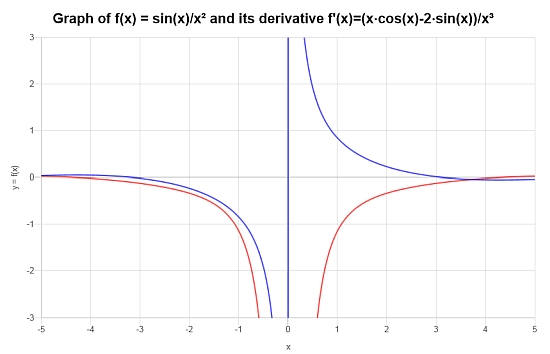
More Derivative Calculators

In Calculus you will find derivatives everywhere you look at. There are thousands of applications involving them making them on the most important tools for Science and Engineering.

You will need to learn about implicit differentiation for different applications often times involving related rates, or in multivariate calculus you will be interested in finding partial derivatives.

Overall, you will find your life easier when dealing with derivatives if you are able to properly handle the most common derivative rules, including the Chain Rule, as well the product rule and quotient rule.