More about Linear Equations

This calculator will help you with graphing a linear equation that you provide. So then, the first step is to provide a valid linear equation, something like 2x + 3y = 4, or you could also provide something that does not come directly simplified, like 2/3 x + y = 4/3 x - 1/2 y + 2. Any valid linear expression will work. .

Once you provide a valid linear equation, the easy part comes in, as all you need to do is to click on "Calculate", and the steps of the process of graphing the linear function will be shown to you.

Linear equations will play an important role in some many operations, including to solve a system of linear equations.

Linear Equation Formula

There are different forms in which you can write a linear equation formula. The most common are the standard form, which is shown below

\[a x + by = c \]

Also, there is the slope-intercept form, which is shown below

\[y = mx + n\]

These two forms can mostly be converted from one to another, except for a couple of exceptions, namely the vertical line expressed by x = a. This line is vertical and it crosses the x-axis at (a, 0). We have that x = a is the standard form of the line, but this line does not have slope-intercept (at least where y is the dependent variable)

What are the steps for graphing a linear equation?

• Step 1: Identify clearly the equation available
• Step 2: See the coefficient that multiplies y, if it is zero, then you have a vertical line
• Step 3: If the coefficient that multiplies y is different from zero, then you solve for y in order to get the slope-intercept form
• Step 4: Using the slope-intercept form, evaluate the function at x = 0 and x = 1, and then you have two points where the line passes through
• Step 5: Draw a line using those two points you found as a guide

One of the clearest ways to draw a line is to have two points where the line passes through, as often times using the slope to guide yourself can be misleading.

Solution of linear equation in one variable

Students are familiar with systems of linear equations, and they more or less understand what needs to be done. But then they wonder about the solution of a linear equation in one variable. Say you have the linear equation in slope-intercept form:

\[y = a + bx \]

So, how do you solve that? Well, it is already solved: For each given value of x, the solution of y is y = a + bx. So provided that \(b \ne 0\), you have infinite solutions to a linear equation.

The situation changes when you have two linear equations, in which case you need to solve both equations simultaneously.

Are linear equations that important?

You bet! Perhaps among the most important in the whole Math. This is because of the simplicity and yet vast range of applications.

Example: Linear Equation Calculator

Get the graph of the following linear equation: \(\frac{1}{3} x + \frac{7}{4} y - \frac{5}{6} = 0\)

Solution:

Get the equation of the line in slope-intercept form

The following equation has been given to us.:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Simplifying the constants:

\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]

Now, putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Now, solving for \(y\), by dividing both sides of the equation by \(\frac{7}{4}\), the following is obtained

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\]

and simplifying we finally get the following

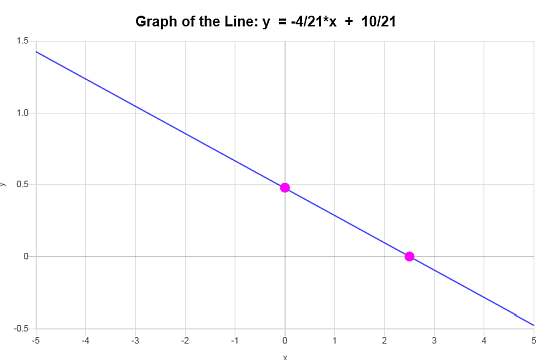
\[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\]

Conclusion: We infer that the equation of the line in slope-intercept form is based on the available data is: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), with a slope of \(\displaystyle b = -\frac{4}{21}\) and y-intercept of \(\displaystyle n = \frac{10}{21}\).

Considering these data, the provided line graph shows

Example: Linear Equation Calculator example

Calculate the following: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\)

Solution: We have now been provided with the following equation:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

The first step is simplify the constants:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]

Putting \(y\) on the left hand side and \(x\) and the constant term on the right hand side so we obtain

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\]

Now, we need to solve for \(y\), and that is achieved by dividing both sides of the equation by \(\frac{5}{4}\), and the following is obtained

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\]

and simplifying we finally get the following

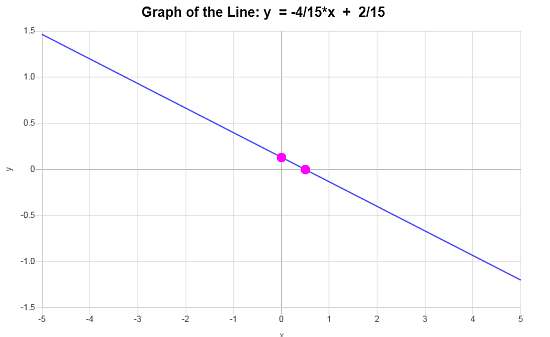
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\]

Conclusion: The line's equation in slope-intercept form is, according to the information provided, \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), with a slope of \(\displaystyle b = -\frac{4}{15}\) and y-intercept of \(\displaystyle n = \frac{2}{15}\).

According to this data, the presented line graph is

Example: Another Linear Equation Calculator example

Does this represent a line: \( y = 5 \). If it does, what are its characteristics?

Solution: Yes it does. Indeed, when you have an expression like \( y = 5 \), you have a linear equation in slope-intercept form, with a = 0 and b = 5. Hence, what we have is a line that is horizontal, that crosses the y-axis at the point (0, 5).

More Algebra calculators

Lines, linear equations and linear functions will always play a crucial role in Algebra, presenting also a clear link with some basic geometric properties.

In terms of applications, perhaps solving systems of linear equations is among the most common application of lines and linear equations.