How to Use this slope calculator with steps

Use this calculator to find the slope of a line that you provide, with all the steps shown.

The slope is a measure of the inclination of the line with respect to the coordinated axes. A positive slope indicates that the line has a upward inclination, whereas a negative slope indicates that the line has a downward inclination.

A slope equal to zero indicates that the line is horizonal, whereas a vertical line does not have a well defined slope.

How to calculate a slope?

Normally the calculation of the slope is easy, but there are multiple ways a slope can be calculated, and it all depends on what information is provided and how it is provided.

The most common ways that a slope calculation is presented is by first providing you with a linear equation for which you need to find its slope, or when they provide you with two points a line passes through.

Slope Calculator from Equation: Finding the slope of the line

This calculator will show you how to compute the slope of a line you provide, and you will have different ways to indicate and define your line. It also will give you a graph reflecting the slope calculated.

For example, one common way is to define your line giving an equation, and then you will have this calculator to compute the slope from the equation.

The general strategy for that is to put the equation of the line in slope-intercept form, from which point is easy to recognize the slope from the structure of the equation \(y = mx + n\).

This is a slope from two points calculator too

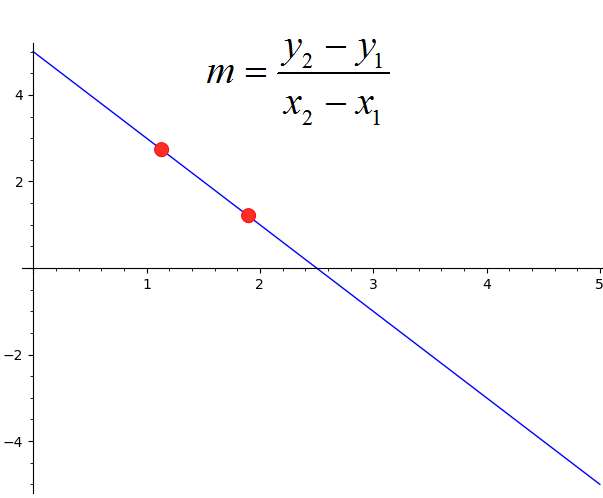
Perhaps one of the most common ways to compute the slope is when you define the equation by providing two points as \((x_1, y_1)\), \((x_2, y_2)\). So, how do you find the slope from two points? Te slope is simply computed as

\[m = \frac{y_2-y_1}{x_2-x_1}\]

which is how to find the slope from two points. Let's not forget that those two points are usually points where a line passes through, so you are finding the slope of the line that passes through those points.

Ultimately, how to find the slope of a line will depend on how the line is defined. This calculator will get you covered with all the cases, even when there are fractions in the calculation.

Interpretation: What is a slope of 2%?

There are several ways of seeing this, but a common way is to think that for each increase in 100 units in X, the line increases 2 units in Y, which explains the 2/100 = 0.02 = 2%.

Along the same line of interpretation, you can say that a slope of 45% is such that an increase of 100 units in X leads to an increase of 45 units in Y. Please notice that this is NOT the same as a slope with 45^o degrees.

Instant Slope Calculator

The idea of a slope calculator is simple when you consider two points, in which case you use the formula above. But what is the instant slope? That refers to the slope when the two points become increasing close.

So you want to see what value the slope approaches too, when the two points approach together. The idea of instant slope is reflected by this derivative calculator, which is essentially computing instant slopes.

Example: Calculation of the slope

Suppose that you have a line that has the following standard form \( \frac{3}{4} x + 2y = 6\). Find slope of the line.

Solution: Calculation of the Slope of a line

We have been provided with the following equation:

\[\displaystyle \frac{3}{4}x+2y=6\]

Putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle 2y = -\frac{3}{4}x +6\]

Now, solving for \(y\), by dividing both sides of the equation by \(2\), the following is obtained

\[\displaystyle y=-\frac{\frac{3}{4}}{2}x+\frac{6}{2}\]

and simplifying we finally get the following

\[\displaystyle y=-\frac{3}{8}x+3\]

Conclusion: Based on the data provided, we conclude that the slope of the line is \(\displaystyle m = -\frac{3}{8}\).

Example: Calculation of Slope from two points

Suppose that you have a line that has passes through 2 points: \( (1, 2)\) and \( (4, 11/3)\). Find slope of the line.

Solution:

Calculation of the Slope of a line

The information provided about the line is that the line passes through the points\(\displaystyle \left( 1, 2\right)\) and \(\displaystyle \left( 4, \frac{11}{3}\right)\)

Therefore, the first step consists in computing the slope. The formula for the slope is: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]

Now, by plugging the corresponding numbers is , we get that the slope is: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{11}{3} - 2}{ \displaystyle 4 - 1} = \frac{ \displaystyle \frac{11}{3}-2}{ \displaystyle 4-1} = \frac{5}{9}\]

So then, we find that the slope is \(\displaystyle m = \frac{5}{9}\) and that the line passes through the point \(\displaystyle \left( 1, 2\right)\)

Conclusion: Based on the data provided, we conclude that the slope of the line is \(\displaystyle m = \frac{5}{9}\).

The slope of a line is one of its most important properties, along with the y-intercept and x-intercept, because they essentially define the line.