More about this Trig Calculator

This trig calculator will allow you to evaluate any trig expression that you provide. Make sure that you provide any valid trigonometric expression,it can be something direct like cos(pi/2), or it could be something that is not fully simplified, like sin(1/3*pi+3/4*pi).

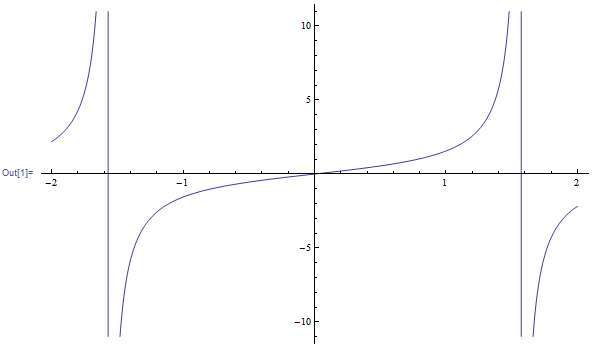
You can also provide a trig function like sin(1/3*pi x +3/4*pi + x) and this calculator will analyze and if possible will deliver the corresponding period, frequency, etc., along with its graph.

Once a valid trig expression has been provided, all you need to do is to click on "Calculate" and all the steps of the calculation will be shown to you.

Trigonometric expressions are quite necessary, especially when you are solving triangles. Usually it is simple to reduce any trig calculation to the calculation of a few notable angles for the cosine and sine.

How to do trig calculations?

Doing a trig calculation can be a very general and broad task, that may have specific strategies that work best depending on the specific trig calculation you need to do and what trig functions are involved, but there are some general strategies that can serve you well.

What are the steps for a trig calculation

• Step 1: Identify clearly the trig expression you want to calculate, and simplify numbers and fraction as much as you can. For example, if you have cos(1+1/2), you will first notice that 1+1/2 = 3/2, so you need actually cos(3/2)
• Step 2: Once possible fractions and simple numbers are grouped and operated if possible, determine whether there are trig functions other than sin and cosine. If there are, express everything in terms of sine and cosine
• Step 3: Now go through all the parts, that now involve only sine and cosine, and assess whether there are notable angles involving multiples or fractions of π
• Step 4: Directly evaluate those expressions with notable angles that can be simplified. Those that cannot be directly simplified (if any) leave as it is, or provide an approximated (rounded value) of them

It is customary to leave as they are expressions that do not have known, simple simplifications. For example, cos(1/4) does not have simple reduction, so it is typically left as it is. But for example, cos(π/3) = 1/2, so such simple reductions are obviously carried out

Trigonometry calculator with steps

The advantage of this calculator is that it will show you all the relevant steps of the process. The process is simple: it is about simplifying expressions that only involve numbers, fractions and overall directly evaluable numeric expressions.

Then, and only then you should go for the trig calculation, so to clear up things as much as possible before attempting any trig calculation. For specific functions, you may want try this sin calculator, that uses the specific characteristics of the sine function.

Advantages of using a trigonometric calculator app

You may think, oh well, I know pretty well my trig functions for basic notable angles, so I don't need a trig calculator app. That may well be the case, though you may hesitate a bit you get presented with something like \(\sin\left(\displaystyle\frac{345}{11}\pi\right)\)....can you simplify it? Is it a notable angle?

It is truly a good thing to try to solve things by hand, and by exercising your trigonometric memory, but a trig calculator app can help you at the very least to check your answers.

Example: Trig Calculation

Calculate the trig expression: \(\sin\left(\frac{5}{4}\pi\right)\)

Solution: The following trigonometric expression has been provided to be calculated:

\[ \sin\left(\frac{5\pi}{4}\right)\]

By inspecting the given trigonometric expression, we can find one notable angle, which is \(\sin\left(\frac{5\pi{}}{4}\right)\).

▹ For the angle \(\frac{5\pi{}}{4}\) we graphically get:

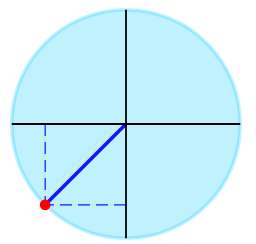
The trigonometric expression given can be simplified as:

Conclusion: We conclude that \(\displaystyle \sin\left(\frac{5\pi}{4}\right) = -\frac{1}{2}\sqrt{2} \approx -0.7071\).

Example: Using the trig calculator

Reduce : \(\displaystyle \cos\left(\frac{1}{3} + \frac{5}{4}\right)\)

Solution: Now we need to work on:

\[ \cos\left(\frac{1}{3}+\frac{5}{4}\right)\]

This trigonometric term can be simplified as follows:

Conclusion: It is concluded that \(\displaystyle \cos\left(\frac{1}{3}+\frac{5}{4}\right) = \cos\left(\frac{19}{12}\right) \approx -0.0125\).

Example: Trig simplification

Calculate \( \sin\left(\frac{2}{3} \times \frac{6}{5} \pi\right)+ \frac{2}{5}\cdot \cos(\frac{\pi}{4}) \).

Solution:By inspecting the given trigonometric expression, we can find one notable angle, which is \(\cos\left(\frac{\pi{}}{4}\right)\).

▹ For the angle \(\frac{\pi{}}{4}\) we graphically get:

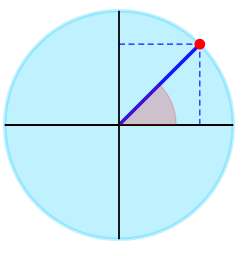
The trigonometric expression given can be simplified as:

Conclusion: We conclude that \(\displaystyle \sin\left(\frac{2}{3}\cdot\frac{6}{5}\pi\right)+\frac{2}{5}\cos\left(\frac{\pi}{4}\right) = \frac{1}{5}\sqrt{2}+\frac{1}{4}\sqrt{-2\sqrt{5}+10} \approx 0.8706\).

More geometry calculators

Working with trig functions is tightly related with working with triangles, so when working with a triangle calculator you will find a lot of trig calculations.