More about this Average Rate of Change Calculator with steps.

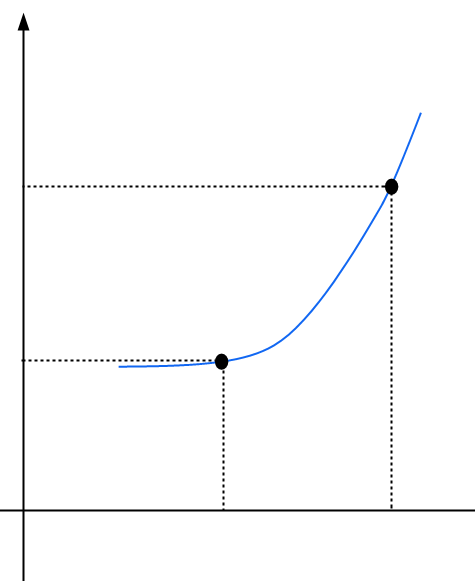
The idea of this net change calculator is to estimate how much the given function changes per unit of time. So, how do you calculate the average rate of change? It is not hard. Indeed, the average rate of change is defined as

\[\text{Average Rate of Change} = \displaystyle\frac{\Delta y}{\Delta t} = \displaystyle\frac{y_2 - y_1}{t_2 - t_1}\]

This is, it corresponds to the ratio of the net change in y (\(\Delta y\)) and the net change in t (\(\Delta t\)).

Is the average rate of change of a function constant?

Not necessarily. The average rate of change is computed over a certain interval. If you change the interval, the average rate of change can perfectly change as well.

Can we say that the rate of change is the same as slope?

Not always. Indeed, that only happens when the function is linear (its graph is a straight line). When the function is not linear, then the "slope" is defined locally by its derivative at each specific point. Also, we need to understand that the average rate of change ultimately is computed over an interval, so it can be changing based on the interval chosen.

The average rate of change measures the slope of the line that passes through two given points \((t_1, y_1)\) and \((t_2, y_2)\). As \(t_1\) approaches to \(t_2\), the average rate of change will look more and more like the slope of the tangent line.

What is the difference with the instant rate of change?

The instant rate of change is obtained when the size of the interval for which the average rate of change is computed becomes smaller and smaller. Technically, the instant rate of change corresponds to the limit of the average rate of change, when the size of the interval approaches to zero, which is associated with the derivative of the function.

Is this a Net change calculator?

Not exactly. A net change calculator compute the difference between the values of a function a two given points, but it is not divided by the difference between the arguments. So, the net change is a measure of an absolute difference, whereas this calculator find the relative change.

So, when do you compute the net change? It is when you need an absolute change as opposed to a relative change that is given by this average rage of change solver.

How is this similar to an instantaneous rate of change?

They are related indeed. An instantaneous rate of change is defined as the limit of the average rate of change, as the difference between the arguments approaches to zero.

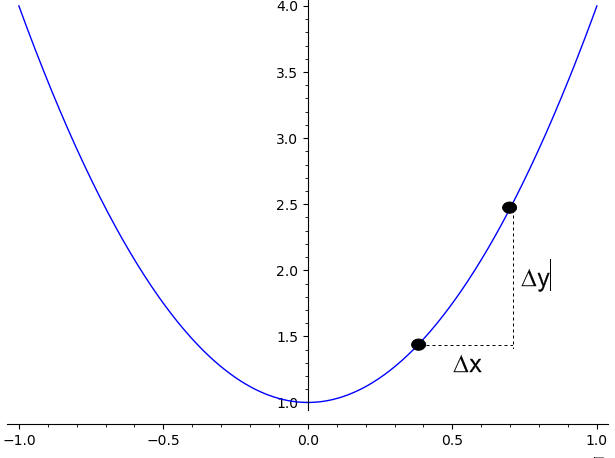
Rate of Change Example

Assume you have a a function that at \(t = 1\) has a value of \(y(1) = 5\), and that at \(t = 4\) has a value of \(y(4) = 10\). Compute the average rate of change in this case.

Solution:

The following is the information we have been provided about the function at times \(t = 1\) and \(t = 4\):

Time 1 \((t_1)\) =	\(1\)
Function at Time 1 \((f(t_1))\) =	\(5\)
Time 2 \((t_2)\) =	\(4\)
Function at Time 2 \((f(t_2))\) =	\(10\)

By definition, the average rate of change is computed as:

\[ \begin{array}{ccl} \text{Average Rate of Change} & = & \displaystyle \frac{\Delta y}{\Delta t} \\\\ \\\\ & = & \displaystyle \frac{y_2 - y_1}{t_2 - t_1} \\\\ \\\\ & = & \displaystyle \frac{ 10 - 5}{ 4- 1} \\\\ \\\\ & = & \displaystyle \frac{ 5}{ 3} \\\\ \\\\ & = & \displaystyle 1.6667 \end{array}\]

Therefore, the average rate of change for a function that passes through the points \((1, 5)\) and \((4, 10)\) is 1.6667.