The Binomial Theorem
The Binomial Theorem is one of the more famous theorems in Algebra, and it has a multitude of applications in the fields of Algebra, Probability and Statistics. It states a nice and concise formula for the n th power of the sum of two values: \((a+b)^n\)
![]() I was first informally presented by Sir Isaac Newton in 1665.
I was first informally presented by Sir Isaac Newton in 1665.
![]() Many other notable mathematicians have tackled the Binomial theorem after Newton. It was a very appealing problem in the 17th and 18th centuries.
Many other notable mathematicians have tackled the Binomial theorem after Newton. It was a very appealing problem in the 17th and 18th centuries.
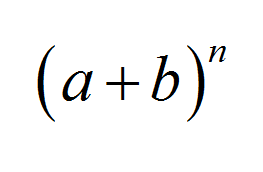
The Formula for the Binomial Expansion
What is integer about the Binomial Theorem is that it provides a very elegant and concise formula. Before getting into the formula, let us do some calculations. For example, for \(n = 2\) we get:
\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]Now let's try with \(n = 3\):
\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]Finally, let us be brave and try it with \(n = 4\):
\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]Ok, that was brave, was it, huh?? Do you see any patterns there. I can see some. For example, for \(n = 2\) we could simplify it to 3 terms. For \(n = 3\) we could simplify it to 4 terms, and for \(n = 4\) we could simplify it to 5 terms. So in general, I expect that for the general power of \(n\), we will have \(n+1\) terms
More patterns? Well, there is always a term of the form \(a^l b^m\), and we can see that the \(l\) powers go decreasing, and the \(m\) powers go increasing. But there is something interesting too: If you check each term, the sum of powers is always \(n\). Indeed, you will check that \(l + m = n\) for all those terms.
For example, for \(n = 2\) you have the term \(2 a b\). The power of \(a\) is 1, and the power of \(b\) is 1, and the sum of powers is \(1 + 1 = 2\). Or for example, for \(n = 4\) you have the term \(6 a^2 b^2\), where the power of \(a\) is 2, and the power of \(b\) is 2, and the sum of powers is \(2 + 2 = 4\)
The General Binomial Theorem
Now we are ready to give the general expression for the Binomial Theorem. Ready? We have:
\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]where the term \({n \choose i}\) reads as "n choose i" or also as a "combinatorial coefficient", and it is defined as
\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]For example,
\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]You can use this combinatorial coefficient calculator to learn more about it and to practicing by seeing all the steps shown.
The General Binomial Theorem using a Summation
The sum above that defines the Binomial Theorem uses the notation by extension, to make the terms more understandable. Like always in Math, we try to make things more compact, and the above expression can be summarized as:
\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]Observe the powers of terms in the expansion. The general term is \(a^i b^{n-i}\) (times a constant). The sum of the powers is \(i + (n-i) = n\). So the sum of the powers of ALL terms in the expansion must be \(n\). Isn't it pretty???
EXAMPLE 1
Can the term \(x^3 y^2\) (times a constant) be part of the expansion of \((x+y)^6\)? Why?
ANSWER:
The answer is no. In this case, \(n = 6\), and we know from the Binomial theorem that the sum of the powers of terms \(x^l y^m\) in the expansion must be equal to \(n\). In this case, \(l + m = 3 + 2 = 5\), which is not the same as \(n = 6\). Hence, the term \(x^3 y^2\) (times a constant) cannot be part of the expansion of \((x+y)^6\).
EXAMPLE 2
Expand \((a-b)^3\) using the Binomial theorem.
ANSWER:
Wait. You must be thinking "You just taught me how to expand \((a+b)^n\), but now you ask me about \((a-b)^n\). Why are you so cruel". Hold on. I am not playing tricks on you.
There is always a trick (don't forget that line, it appears in Math a lot).
![]() Observe that \(a - b\) is the same as \(a + (-b)\).
Observe that \(a - b\) is the same as \(a + (-b)\).
Ahhhhhhh, so the Binomial Theorem still applies. So then:
\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]More About the Binomial Expansion
The Binomial theorem is so important, that it is covered in mostly all courses including Algebra, Calculus, Probability and Statistics.
There are some generalizations like the negative binomial expansion, which is beyond the scope of this tutorial.
The Pascal Triangle
Some times students get stuck when they need to compute the constants (the combinatorial coefficients) that go in the binomial expansion. One really easy way to do it is to use the Pascal Triangle.
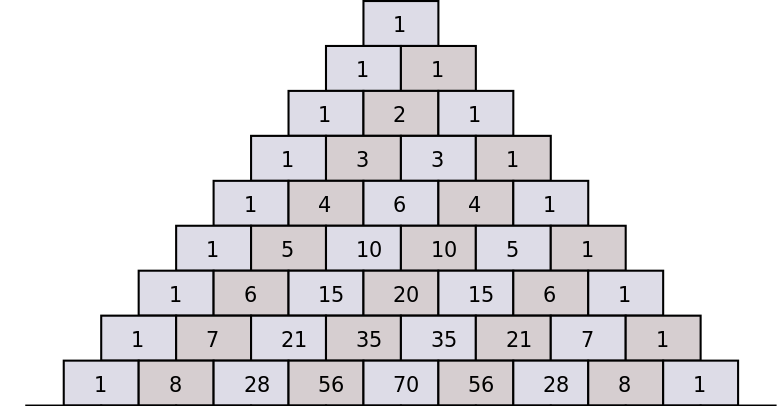
The Pascal triangle shows how the successive binomial coefficients can be computed based on the coefficients of the previous value of \(n\), by adding the two coefficients that come immediately above.
Applications
The binomial expansion has multiple applications in Algebra and in Probability Theory. For example, in Probability, the Binomial distribution is based upon the binomial theorem.
Indeed, consider a number \(0 \le p \le 1\). Then, \(p + (1-p) = 1\) and we can use the Binomial theorem:
\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]which means that
\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]It turns out that each of the terms \({n \choose i} p^i (1-p)^{n-i}\) represents a probability. Moreover, we have:
\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]where \(X\) is the number of successes after \(n\) trials, when the probability of success of each trial is \(p\). The \(X\) variable is known as the binomial random variable.
Related Calculators
You can also compute probabilities for binomial distribution using this calculator . Also, you may want to compute permutation coefficients , that are related to combinatorial coefficients.
