Rules of Exponents
The operations with exponents are among the most common operations you will be conducting all around in Math, and it is crucial that you have a proper foundation about them.
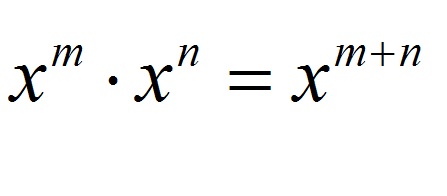
![]() Without further ado, let us list the basic exponent properties. Using these properties proficiently is of the utmost importance. The rules are:
Without further ado, let us list the basic exponent properties. Using these properties proficiently is of the utmost importance. The rules are:
Rule 1: \(\large \displaystyle x^0 = 1\), for \(x = \not 0\)
Rule 2: \(\large\displaystyle x^1 = x\)
Rule 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Rule 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Rule 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Rule 6: \(\large\displaystyle (x \cdot y)^m = x^m \cdot y^m\)
Let us explain a little bit these rules in words .
![]() Rule 1
is saying that anything raised to the power of zero is equal to 1. Well, except for 0, because by convention (and there is a good reason for it) \(0^0 = 0\).
Rule 1
is saying that anything raised to the power of zero is equal to 1. Well, except for 0, because by convention (and there is a good reason for it) \(0^0 = 0\).
![]() Now,
Rule 2
is saying that taking any number and raising it to the power of 1 gives the same original number. In other words, raising a number to the power of 1 does not affect the number.
Now,
Rule 2
is saying that taking any number and raising it to the power of 1 gives the same original number. In other words, raising a number to the power of 1 does not affect the number.
![]() Rule 3
is saying that when I multiply powers with the same base, the result is a power that has the same base, raised to a power that corresponds to the sum of the exponents of the powers that I am multiplying.
Rule 3
is saying that when I multiply powers with the same base, the result is a power that has the same base, raised to a power that corresponds to the sum of the exponents of the powers that I am multiplying.
![]() Rule 4
is saying that taking the power of a power is the same as taking one power with the multiplied exponents as the exponent.
Rule 4
is saying that taking the power of a power is the same as taking one power with the multiplied exponents as the exponent.
![]() Rule 5
is saying that when I divide powers with the same base, the result is a power that has the same base, raised to a power that corresponds to the subtraction of the exponents of the powers that I am multiplying.
Rule 5
is saying that when I divide powers with the same base, the result is a power that has the same base, raised to a power that corresponds to the subtraction of the exponents of the powers that I am multiplying.
![]() Rule 6
is saying that when I have a power affecting a multiplication, then it is the same as multiplying each of the terms raised to that power.
Rule 6
is saying that when I have a power affecting a multiplication, then it is the same as multiplying each of the terms raised to that power.
EXAMPLE 1
Simplify the following expression
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2}\]ANSWER:
Using Rule 5 for the division of powers with the same base:
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2} = \frac{x^{3}y^{3}}{x^{1/2} y^2} \] \[\large \displaystyle = \frac{x^3}{x^{1/2}} \cdot \frac{y^3}{y^2} = \displaystyle x^{3-1/2} \cdot y^{3-2}\] \[\large \displaystyle = \displaystyle x^{5/2} \cdot y^{1} = x^{5/2} y\]Should I Worry About Negative Exponents?
Not really. First of all, the 5 rules for exponents stated above do not make any specific statement about that the exponents need to be non-negative. In fact, the rules work all the same of the exponents are negative.
Indeed, for negative exponents , there will be two rules that will allow you to transform them into positive exponents:
\[\large\displaystyle \frac{1}{x^n} = x^{-n}\]
![]() This above expression is showing us that we can convert a power with a negative exponent that is in the numerator to a power in the denominator with the corresponding positive exponent.
This above expression is showing us that we can convert a power with a negative exponent that is in the numerator to a power in the denominator with the corresponding positive exponent.
![]() This above expression is showing us that we can convert a power with a negative exponent that is in the denominator to a power in the numerator with the corresponding positive exponent.
This above expression is showing us that we can convert a power with a negative exponent that is in the denominator to a power in the numerator with the corresponding positive exponent.
EXAMPLE 2
Simplify the following expression, leaving no negative exponents:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}}\]ANSWER:
Transforming the negative exponents into positive exponents, and applying the 5 exponent rules:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}} = \frac{x^{4} x^{1/2} y^{-2}}{x^{-3/2} y^{1/2}} \] \[\large \displaystyle = \frac{x^{4} x^{1/2} x^{3/2}}{y^{1/2} y^{2}} = \frac{x^{4+1/2+3/2}}{y^{2+1/2}} \] \[\large \displaystyle = \frac{x^{6}}{y^{5/2}} \]which concludes the simplification.
Are These Exponent Rules Somewhat Related to the Rules of Logarithms?
Absolutely! Check out the logarithmic rules and you will find out that they are structurally very similar, and this is because the logarithms and powers are inverse operations to each other.
Just as a little sample, let's do a quick proof. Assume that \(a = x^m\) and \(b = x^n\). Then, by definition, \(m = \log_x a\) and \(n = \log_x b\). So then, by the exponent rules, \(a\cdot b = x^m \cdot x^n = x^{m+n}\). Hence, by definition, \(m + n = \log_x (a \cdot b)\). But \(m = \log_x a\) and \(n = \log_x b\), so then \(\log_x a + \log_x b = \log_x (a \cdot b)\).
More About the Rule of Exponents
One thing were we need to make an emphasis is on the fact that the rules for exponents do not require the exponents to be positive. The exponents do not need need to be integer. The rules hold for real exponents.
• Do not forget that if you are dealing with a negative exponent in the numerator, you can transform it by passing it to the denominator with positive exponent.
• Also, if you are dealing with a negative exponent in the denominator, you can transform it by passing it to the numerator with positive exponent.
The rules of exponents have so many applications, including providing a base ground for obtaining the rules for simplifying radicals , which come as a corollary of the roots of exponents.
In graphical terms, you can explore this rule by graphing different exponential functions , and seeing the specific properties they have.
