More about this parallel lines calculator tool.

Geometrically speaking, two lines are parallel when they don't intersect, or they potentially are the same line. So then, if you graph the two lines, you will visually see that they don't intersect. But that can be tricky.

But naturally, there are algebraic ways to assess whether or not two lines are parallel. One of the simplest way is to use the slope criterion.

How to determine if two lines are Parallel?

There are a couple of ways:

1. Graphically: Take a look at the graph, and if the lines don't intersect, then the lines are parallel
2. Algebraically: Compute the slope to each of the lines. If they have the same slope, the lines are parallel

The advantage of the graphical method is that it is simple, and it involves just taking a look at the graph, but naturally, in order to do so, you need to construct the graphs.

A disadvantage of the graphical method is that your eyes can deceive you. It may seems that the graph of lines do not intersect, but perhaps you are not graphing a big enough portion of the line.

An advantage of the algebraic method is that it is unequivocal. If the slopes coincide, the lines are parallel, and if they don't, then the lines are not parallel.

The one disadvantage of the algebraic method is that you need to take the work of formally computing the slope.

Parallel line equation

Observe that lines that are parallel will have the same slope. So if the equation of a line is \(y = a x + b\), what is the equation of the parallel line?

First, there is not one parallel line, there are actually infinite parallel lines, and the equation is \(y = a x + c\), for any \(c\).

As we can see, \(y = a x + b\) and \(y = a x + c\) both have a slope equal to "a", so they are parallel.

If you don't have the lines already in slope-intercept format, you can always solve for y, or solve for x is you want to reverse the axes.

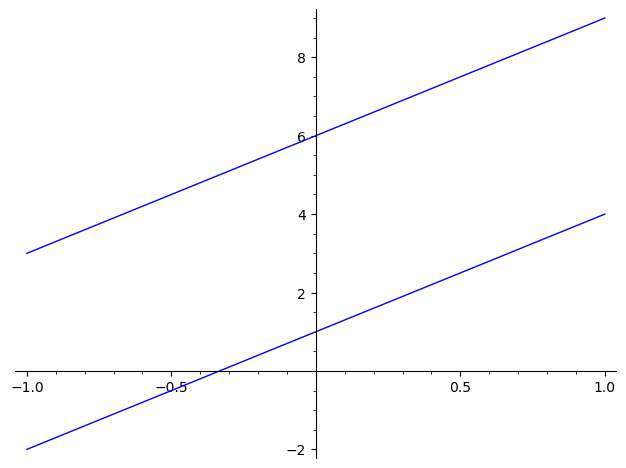
The slope criterion

Two lines are parallel if they have the same slope. So that is the easiest way to go about determining if two lines are parallel, you simply compute the slope of both lines and check whether they are the same or not.

One exception is the case of two vertical lines, which are parallel, although we cannot compare the slopes because they are undefined.

If you have something like the slope-intercept form of the lines already given, you can directly assess whether or not the lines are parallel. Otherwise, you need the extra step of computing the slopes before comparing them.

Geometric interpretation of the graph of two parallel lines

Two lines that are parallel correspond to a system of equations with no solutions (or infinite solutions), where each equation represent one line.

Also, when the lines are not parallel they will intersect at one point and at one point only, which corresponds to a system of equations with a unique solution.

Example

Determine whether or the lines \(2x + 3y = 1\) and \(x + y = 3\) are parallel.

Answer:

First Line: Put the first equation in slope-intercept form

We have been provided with the following equation:

\[\displaystyle 2x+3y=1\]

Putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle 3y = -2x +1\]

Now, solving for \(y\), the following is obtained

\[\displaystyle y=\frac{-2}{3}x+\frac{1}{3}\]

and simplifying all the terms that need simplification, we finally get the following

\[\displaystyle y=-\frac{2}{3}x+\frac{1}{3}\]

Second Line: Put the second equation in slope-intercept form

We have been provided with the following equation:

\[\displaystyle x+y=3\]

Putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle y = -x +3\]

Analyze and Compare Slopes

Based on this information, we find that the slope of the first line is \(m_1 = -\frac{2}{3}\) and the slope of the second line is also \(m_2 = -1\), which are unequal, so then the lines are NOT parallel.

Notice that if perpendicularity is what you are looking for, you can use this perpendicular line calculator. By definition, perpendicular lines are not parallel, because perpendicular lines have different slopes ALWAYS.