About this sin calculator

This sin calculator will two the following for you: you can provide a numeric expression such as sin(pi/4), in which case the calculator will simplify it, and will give an approximate numeric value if necessary. Also, if you provide a sin function like sin(3x+1), the calculator will graph it.

Then, the process is simple: once you have provided the sin expression you want to calculate, you just click on the "Calculate" button that is below the form to get the steps of the solution.

Sine, along with cosine are two corner stones of trigonometry. You will see sine and cosine all around when solving triangles, for example, but also in fields like Physics.

How do you calculate sin?

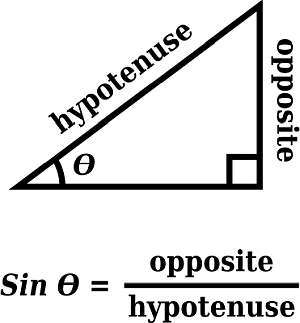
Sin is one of the basic building blocks in Geometry and Trigonometry. Sin is a quantity that can be computed for angles in the context of a right triangle. When you have one of angles in a right triangle that is not the 90_o one, you can find the opposite side and the adjacent side.

Then, the formula for sin is

\[\sin \theta = \frac{\text{Opposite Side} }{ \text{Hypothenuse} }\]

What is sin equal to?

Sin is a dimensionless amount, that measures the size of the inclination of an angle with respect to the horizontal reference, where the adjacent side is sitting.

When sin is zero, then the angle is zero, so there is no opening. The maximum opening of the angle happens when sin = 1, which occurs at 90_o.

What is sin of 1?

That question may seem as an innocent one, but it often times lead to confusion. In formal Math, all trigonometric functions will be measured in radians by default. But for some reason, radians are not well known or too popular among students, who prefer to use degrees as a measure, because it is simply more familiar.

Students know well the notable angles in degrees like 90_o being the right angle, and 360_o being the full circle. You can use this degree to radian calculator to move around between the two systems.

So, the correct answer to what is sin(1) is that sin(1) is approximately 0.841471, when the angle 1 is assumed to be in radians. Now, sin(1) is approximately 0.017452 when 1 is assumed to be expressed in degrees. So then, extreme care should be exercised when dealing with angles.

What is sine to the negative 1?

Another question that formally has a simple answer, but sometimes is depends on the convention used. Sine to the negative 1 needs to be further specified, as sine is a function. So you can do sin(1), and that is a number, and sin(1) to the negative 1 is just taking the inverse of the number sin(1), so you have 1/sin(1), which is a number.

Often times though, sine to the negative 1 is meaning to refer to the 'inverse function of sine', which is known as the arcsin function, or sometimes some people like to use the nomenclature of \(sin^{-1}(x)\).

Can I use a scientific calculator to calculate sin

Indeed you can, but one advantage of using this sin calculator is that you will get the steps shown along with the result. Most calculators will only show the final answer.

How to use a sin calculator?

The main idea of a sin calculator is to evaluate sin expressions that you provide. The are some notable angles, usually multiples or fractions of \(\pi\) that are simple, integer or fraction results when calculating their sin, so it is a good idea to use a sin expression calculator to help you with that.

It is not easy to remember all the sin calculations for ALL notable angles, and you will end up working with a triangle, trying to get the answer manually, and a calculator will come in handy to double check what you obtain manually.

Also, you can instead feed the calculator with a sin function, like sin(pi x), and rather than evaluating a few points, this calculator will give you the corresponding graph

What are the steps for using a sin calculator?

• Step 1: Identify the sin expression you want to calculate
• Step 2: Type the expression in the corresponding box. You don't need to pre simplify, the calculator will do it for you
• Step 3: The calculator will check whether it is an expression that can be evaluated, in which case if will reduce to its simplest terms
• Step 4: If sin is still in the expression because it could not be simplified any further, like sin(3/4), the calculator will give you an approximated numeric value
• Step 5: If a sin function is provided instead, a graph will be provided

We cannot emphasize enough the importance of correctly calculating operations involving sine, as those will appear literally everywhere.

sin and cos formula

Sine and cosine are two very close cousins, if not sisters. There is tight relationship between them, expressed in the following formula:

\[\displaystyle \sin\left(\frac{\pi}{2} - x \right) = \cos(x) \]

Also, another formula that initimately links sine and cosine is:

\[\displaystyle \sin^2(x) + \cos^2(x) = 1 \]

Why is sin so important?

Sines are important because, along with cosines are at the center and core of the construction of a circle. And then circles harbor many other constructions, like triangles and so on.

Sine and cosine end up entangled in every single geometric construction, consequently.

Example: Sin calculator

Calculate the following sin expression: \(\sin\left(\frac{\pi}{3}\right)\)

Solution: The following trigonometric expression has been provided to be calculated:

\[ \sin\left(\frac{\pi}{3}\right)\]

By inspecting the given trigonometric expression, we can find one notable angle, which is \(\sin\left(\frac{\pi{}}{3}\right)\).

▹ For the angle \(\frac{\pi{}}{3}\) we graphically get:

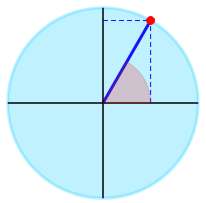
The trigonometric expression given can be simplified as:

Conclusion: We conclude that \(\displaystyle \sin\left(\frac{\pi}{3}\right) = \frac{1}{2}\sqrt{3} \approx 0.866\).

Example: More sine calculations

Calculate the following: \( \sin\left(\frac{5}{4}\right) \)

Solution: The following trigonometric expression has been provided to be calculated:

\[ \sin\left(\frac{5}{4}\right)\]

but this given trigonometric expression cannot be further simplified.

Conclusion: The passed function cannot be simplified, and we get that approximately \(\displaystyle \sin\left(\frac{5}{4}\right) \approx 0.949\).

Example: Sin function

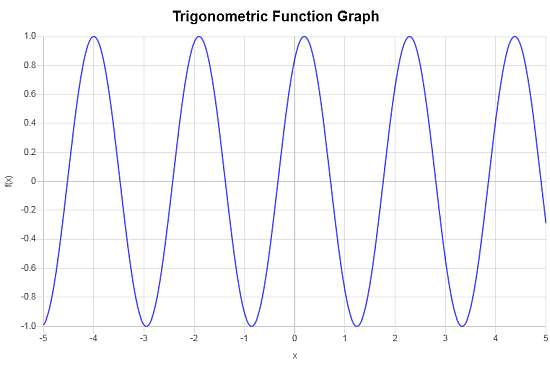
Calculate \( \sin(3x + 1) \).

Solution: We need to work with the following trigonometric function

\[f(x) = \sin\left(3x+1\right)\]

Based on the argument of the trigonometric function that was passed, the frequency and the period are computed as follows:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{3} \\\\ \\\\ & \approx & 2.0944 \end{array}\]

and also

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{3}{2\pi} \\\\ \\\\ & \approx & 0.4775 \end{array}\]

Based on the provided trigonometric function, \(f(x) = \sin\left(3x+1\right)\), we obtain that:

» The amplitude in this case is \(A = 1\).

» The phase shift is equal to \(\displaystyle\frac{-1}{3} = -0.3333\).

» The vertical shift is equal to \( 0\).

Summarizing, the following has been found for the given trigonometric function

• Period = \(2.0944\)
• Frequency = \(0.4775\)
• Amplitude = \(1\)
• Phase Shift = \(-0.3333\)
• Vertical Shift = \(\displaystyle 0\)

The following is the corresponding graph

More trigonometric calculators

Trigonometry blend all these concepts together, including circles and triangles, and both sin and cos are at the very core of it.

Dealing with trigonometric expressions is another crucial skill that is very important for you to acquire.