More about this linear equation grapher

Graphing lines is fundamental ability and this calculator will help you with that. You need to start by providing the linear equation you want to graph.

You can provide any linear equation explicitly, for example, x + 3y = 2 , or something that is not fully simplified like x + 3y = 2/3 x.

Graphing lines has so many applications, that it becomes a very practical skill to acquire. Geometrically, lines have a very simple intuition that makes it easy to graph since we don't need much information to specify them.

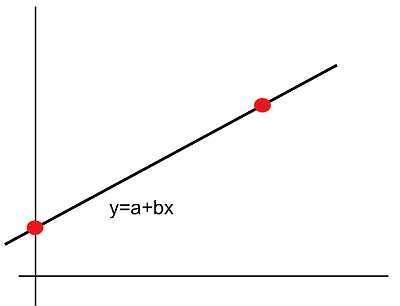
How to graph linear equations?

You can use this graphing calculator to graph lines. If you choose to do it manually, you need to be aware that the approach requires a preamble that will depend on the type of information provided.

What are the steps for graphing a line?

• Step 1: Identify the type of information provided. Do you have an actual equation provided, you have two points, a point and the slope, slope and y-intercept? Clearly assess that
• Step 2: Regardless of the info provided, use it to find two points where the line passes through. For an equation given, solve for y for x = 0 and x = 1 for example. For slope and y-intercept you construct the equation y = a + bx and find two points. If you have one point and slope, define y = y1 + b(x-x1), and plug it at x = 0
• Step 3: Once you have two points where the line passes through, use a ruler to trace a line passing through them

Lines are super easy to draw, just you need to be methodical and be aware of the type of information you have available.

Even if you do it by hand, it is always nice to have a handy linear graphing calculator online to check your results.

Graphing Lines

Graphing lines has so many applications. For example, you can solve a system of equations by graphing the corresponding lines and seeing where they intersect.

Using that method, when the lines are parallel and don't intersect, there will not be any solutions.

Similar to what happened with addition and subtraction, dividing fractions is just derived from the multiplication of fractions: To divide two fractions, you just multiply first one by the inverse fraction of the second one (the inverse fraction is obtained by swapping the numerator by the denominator in the fraction).

Other applications of linear graphs

Lines or linear graphs are truly present everywhere. Linear functions appear in applications all the time, in Calculus and Optimization, so they are truly useful.

Example: Linear Equation Grapher example

Graph the following equations: \(\frac{1}{2}x + \frac{7}{4}y = 0\)

Solution: We need to work with the following equation:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

Working first with the constants:

\[\displaystyle \frac{1}{2}x+\frac{7}{4}y=0\]

The result is obtained by placing (y) on the left side and (x) and the constant on the right side:

\[\displaystyle \frac{7}{4}y = -\frac{1}{2}x \]

Then the process is continued by solving for \(y\), and then by dividing both sides of the equation by \(\frac{7}{4}\). We then get:

\[\displaystyle y=-\frac{\frac{1}{2}}{\frac{7}{4}}x\]

and after simplification, the result is as follows.

\[\displaystyle y=-\frac{2}{7}x\]

Conclusion: We infer that the equation of the line in slope-intercept form that is based on the available data is \(\displaystyle y=-\frac{2}{7}x\), with a slope of \(\displaystyle b = -\frac{2}{7}\) and y-intercept of \(\displaystyle n = 0\).

Hence, the graph of the line provided is

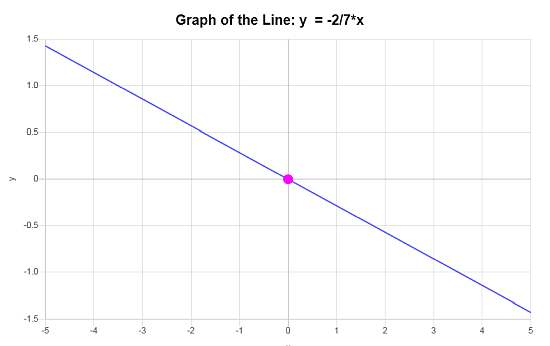
Example: Linear Equation Grapher example

Get the line that represents: \(\frac{2}{3}x + \frac{5}{4}y = - \frac{5}{6}x + 2\)

Solution: We have been provided with the following equation:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Working with the constants:

\[\displaystyle \frac{2}{3}x+\frac{5}{4}y=-\frac{5}{6}x+2\]

Now, putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle \frac{5}{4}y = \left(\frac{-5}{6}-\frac{2}{3}\right)x +2\]

Now, the term multiplying \(y\) is \( \frac{5}{4} - 0 = \frac{5}{4}\), and also since \( -\frac{5}{6} - \frac{2}{3} = -\frac{3}{2}\), the following is obtained

\[\displaystyle \frac{5}{4}y=-\frac{3}{2}x+2\]

Now, solving for \(y\), by dividing both sides of the equation by \(\frac{5}{4}\), the following is obtained

\[\displaystyle y=-\frac{\frac{3}{2}}{\frac{5}{4}}x+\frac{2}{\frac{5}{4}}\]

and simplifying we finally get the following

\[\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\]

Conclusion: Based on the data provided, we conclude that the equation of the line in slope-intercept form is \(\displaystyle y=-\frac{6}{5}x+\frac{8}{5}\), with a slope of \(\displaystyle b = -\frac{6}{5}\) and y-intercept of \(\displaystyle n = \frac{8}{5}\).

The linear graph is

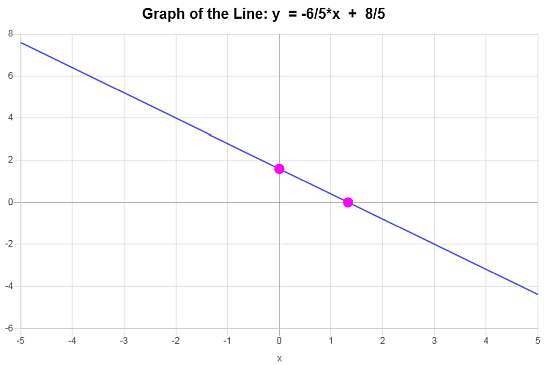
More line calculators

Lines are so important that they deserve their own section in the book of Math. You can compute linear equations in different forms, depending on the specific needs.

Determining lines ultimately will need two points where the line passes through, which can be given directly or indirectly.