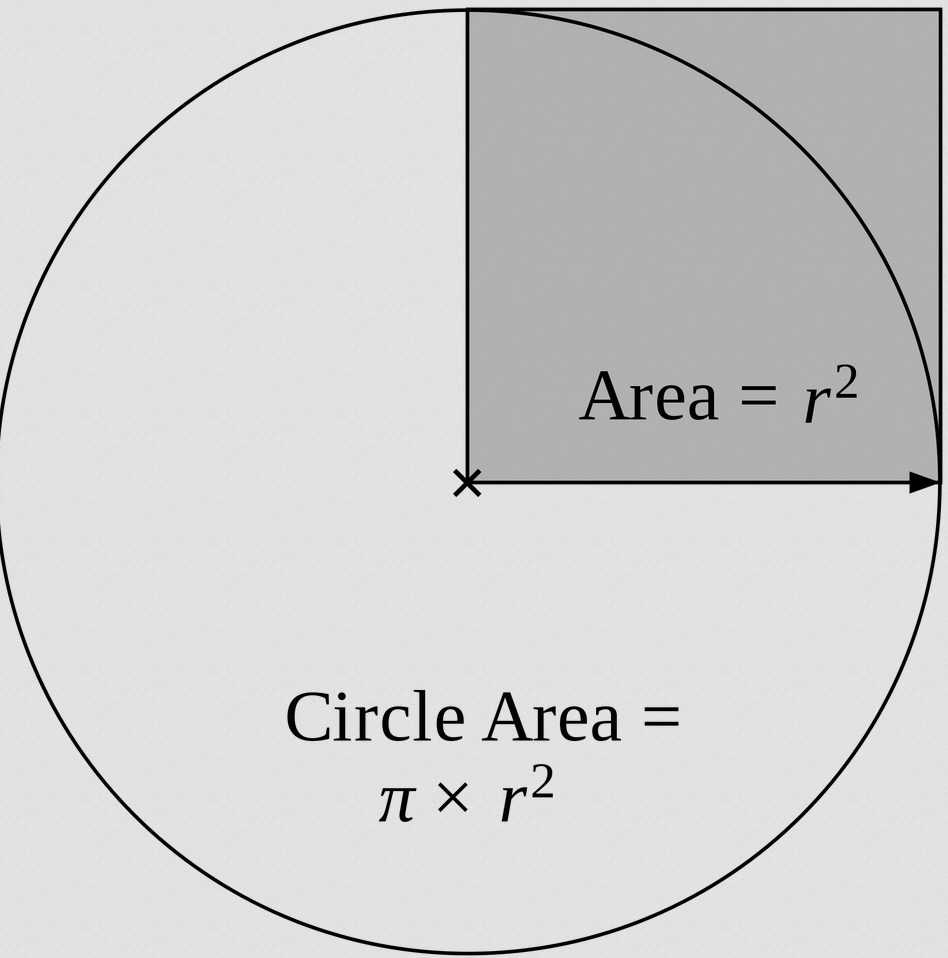
Area of a Circle
Instructions: Use this calculator to find the area of circle, with a given radius r, using the circle formula \(A = \pi r^2\). Please provide the radius in the form box below.
More about this area of a circle calculator
With this calculator you will be able to compute the area of a circle, when you have provided for the radius, \(r\). The provided radius can be a any positive number, or positive algebraic expression. For example, you can type '3.4', or '2*sqrt(3)'. Invalid entries would be '-2' because it is negative, or 'x', because it is not numeric.
After you have provided a valid radius, you can click on "Calculate", and all the steps of the calculation process will be shown, along with a graphical representation.
One different thing you need to circles that you don't need when computing the area of the square or the area of a rectangle, is the use of the constant \(\pi\).

How do compute the area of a circle?
There is a famous area of a circle formula, which is the formula that we all know for the area of the circle. The formula is:
\[\text{Area} = \pi r^2\]This is, the formula involves squaring the radius r, and multiplying that by the constant \(\pi\). What is pi (π)? Well, that is material for another article.
What are the steps for computing the area of a circle
- Step 1: Identify the radius of the circle, and call it 'r'
- Step 2: Once you know the radius 'r', the area of the circle is computed as π * r²
- Step 3: If needed, identify the units of 'r' (if any) and give units to the area
Why would you calculate the area of a circle?
The circle is one of the most important geometric shapes that there exists, and long squares, rectangles are triangles are among the notable shapes that you should be well acquainted with.
Circles and circumferences play a super important role in manufacturing process, as a large proportion of manufactured goods are produced with many rotational processes, where the circle is the main protagonist.
Example: Calculating the area of a circle
Calculate the area of circle with radius r = 3.
Solution: We first need to identify the radius of the circle, which in this case is clearly specified to be r = 3. The formula for the area is:
\[\text{Area} = \pi r^2\]Now, we plug the value of r = 3 into the formula:
\[\text{Area} = 3^2 \pi = 9 \pi\]Example: Another area calculation
Calculate the area of circle with a diameter d = 9.
Solution: In order to use the formula for the area that we have, we first need to know what is the radius. In this case, we are given the diameter instead. But we do know that the radius is equal to half the diameter, so then \(r = \displaystyle\frac{d}{2} = \displaystyle\frac{9}{2} \) .
Now, we plug the value of \(r = \displaystyle\frac{9}{2} \) into the formula:
\[\text{Area} = \pi r^2 = \left(\displaystyle\frac{9}{2}\right)^2 \pi = \displaystyle\frac{81 \pi}{4} \]Example: Area of a circle with units
Calculate the area of circle with a radius of r = 2 cm
Solution: We first identify the radius and we see that r = 2 cm, so we have the radius, but we also have units (cms). Then, by plugging r = 2 cm into the formula:
\[\text{Area} = \pi 2^2 \,\, cm^2= 4 \pi \,\,cm^2\]Other useful area calculators
Geometric shapes with straight boundaries will tend to have easier calculation processes. Indeed, calculating the area of a rectangle, the area of a square, the area of a rhombus, and the area of a triangle will all require the same methodology, but that cannot be applied to a circle, for example.
In a similar category as the circle is the calculation of the area of an ellipse, which comes with the simplification of a very complicated calculation.