Period and Frequency Calculator

When dealing with periodic functions, there are some crucial parameters that need to be computed, and these are the period (\(P\)) and the frequency (\(f\)).

The period \(P\) of a periodic function corresponds to the number that satisfies the following property:

\[f(x+P) = f(x)\]

for all values of \(x\). Observe that not all functions have a period. Those who do are called periodic functions .

Period of some common functions

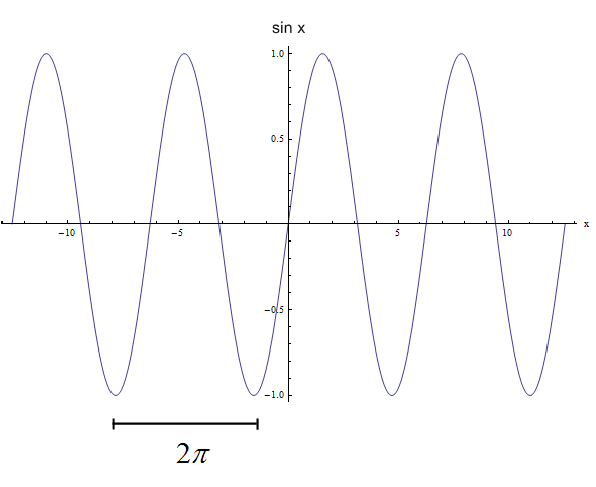
Trigonometric functions are examples of periodic functions. For example, if we consider function, \(f(x) = \sin x\), its period is \(2\pi\), as shown in the graph below:

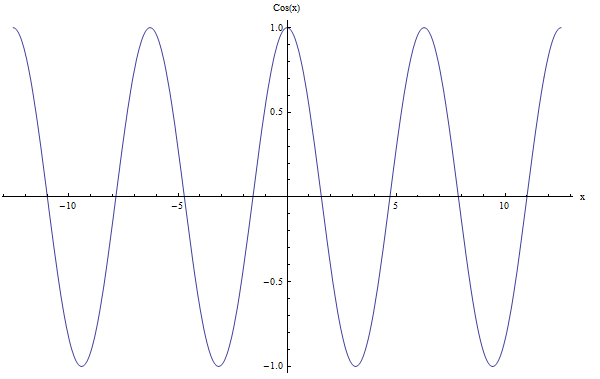
For \(\cos x\) we also have the the period is \(2\pi\). Check out the graph below:

Period of Other Trigonometric Functions

Recall that the cosecant function \(\csc x\) is the inverse of \(\sin x\), this is \(\csc x = \frac{1}{\sin x}\), so then the period of \(\csc x\) is also \(2\pi\).

Similarly, the secant function \(\sec x\) is the inverse of \(\cos x\), this is \(\sec x = \frac{1}{\cos x}\), so then the period of \(\sec x\) is \(2\pi\) as well.

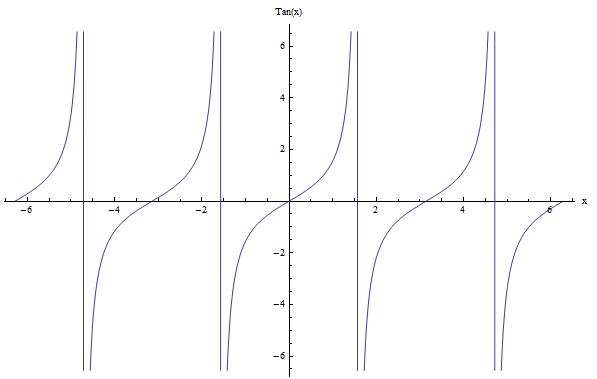
How about the tangent? The tangent function \(\tan x\) is slightly different because its period is \(\pi\). Indeed, its graph looks different than those of the sine and cosine, but tangent is also periodic. One difference is that \(\tan x\) has discontinuities. Check it out:

Similarly as before, the cotangent function \(\cot x\) is the inverse of \(\tan x\), with \(\cot x = \frac{1}{\tan x}\), so then the period of \(\cot x\) is also \(\pi\).

Calculation of the Frequency

Another important element to consider for periodic function is the frequency (\(f\)), which is calculated in terms of the period \(P\) as:

\[f = \frac{1}{P}\]

So the frequency is the inverse of the period. And vice-versa, the period is the inverse of the frequency.

For example, what is the frequency of \(\sin x\)? Following the above formula, since we know that for sine the period is \(P = 2\pi\):

\[f = \frac{1}{P} = \frac{1}{2\pi} \approx 0.1592\]

This calculator will also compute the amplitude, phase shift and vertical shift if the function is properly defined. Those parameters pretty determine the behavior of trigonometric function.

If you need to graph a trigonometric function, you should use this trigonometric graph maker .