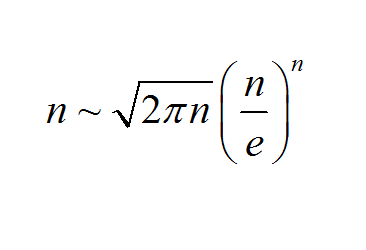Stirling Approximation Calculator
Instructions: Use this Stirling Approximation Calculator, to find an approximation for the factorial of a number \(n!\). Please type a number (up to 30) to compute this approximation.
Stirling Approximation Calculator
Stirling Approximation is a type of asymptotic approximation to estimate \(n!\). What is the point of this you might ask? After all \(n!\) can be computed easily (indeed, examples like \(2!\), \(3!\), those are direct).
Well, you are sort of right. The problem is when \(n\) is large and mainly, the problem occurs when \(n\) is NOT an integer, in that case, computing the factorial is really depending on using the Gamma function \(\Gamma\), which is very computing intensive to domesticate.
That is where Stirling's approximation excels. The approximation is
\[n! \approx \displaystyle\sqrt{2\pi n}\left(\frac{n}{e}\right)^n\]