Horizontal Line Test

This calculator will allow you to run the horizontal line test for any given function you provide, showing steps. The function you provide could be something like 'y = 2x - 1', which is the simplest kind of linear function you can find, or you can provide a more complex function like 'y = (2x-1)/(x+1)' which involves a rational function.

Once you provide a valid function, you can click on the "Calculate" button, and you will be provided with all the steps of the process, indicating whether or not the function passes the horizontal line test (HLT).

The way this calculator works is by setting a generic horizontal line, and checking how many times (if ever at all) the line crosses this given arbitrary horizontal line. This involving solving for x the equation y = f(x).

What is the Horizontal Line Test?

The HLT is a test that allows you to assess whether or not a function is one-to-one. It consists of drawing horizontal lines at different heights and seeing where they cross the graph of the given function f(x), if they do at all.

If no horizontal line that you can imagine will cross the graph of the function f(x) more than once, then the function is one-to-one. On the other hand, if you are able to find a horizontal line that will cross the graph of the function f(x) MORE THAN ONCE, then you have proven that the function is NOT one-to-one

So then you may be thinking "Wait a minute", this tool does not work really to prove that a function is one-to-one using the horizontal line test, but rather to prove that IT IS NOT one-to-one using it.

Because, in practicality, I cannot possibly graph ALL the horizontal lines there are to check how many times they cross the graph of f(x), but if I find ONE horizontal line that crosses the graph of f(x) too many times, then I know it is not one-to-one. So, good thinking, you are onto something good there.

Using the Horizontal Line Test in Practicality

For example, if you have the function \(f(x) = x^2\), then the graph would look more or less like:

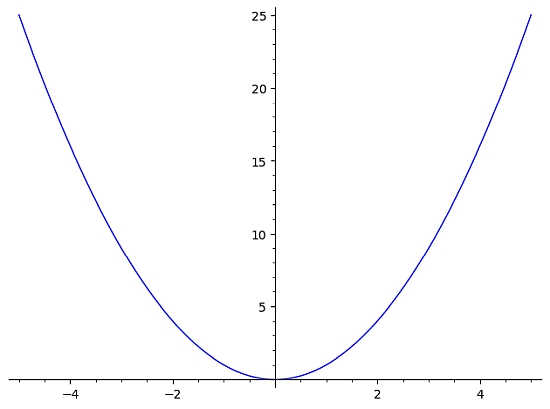
In this case, we see right away that this function fails the horizontal line test. Why, because the horizontal line y = 10 shown in the graph below crosses the graph of f(x) twice (more than once)

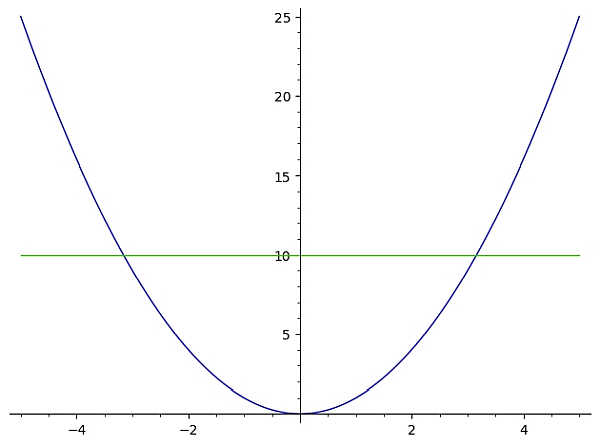
In this case, the function \(f(x) = x^2\) fails the horizontal line test and therefore, it is not a one-to-one function.

Now, since it is impossible to test ALL possible horizontal lines, the HLT needs to attempted using algebraic means, unless you visually see a clear case of a horizontal line that will make the function fail the test.

Using the Horizontal Line Test (Analytically)

• Step 1: Start with a given valid function f(x), you will set the level of a horizontal line at an arbitrary value of y
• Step 2: So you set the equation: y = f(x), and the objective is to solve for x
• Step 3: There is not one strategy to solve this equation, as it depends on the nature of the function f(x). If f(x) is a simple linear or quadratic function, then it is quite easy to solve for x. If not, then different methods need to be tested
• Step 4: If when solving for x you find more than one solution for an arbitrary y, then the function fails the HLT. Otherwise, if there is one solution or no solution, it passes it.

Subtracting fractions is just derived by the sum of fractions: To subtract two fractions, you just multiply the second one by -1, and the add it to the first.

Can the horizontal line take negative or positive values?

The main key of the analytical implementation of the HLT is that you choose an arbitrary horizontal line. It can be arbitrary value, either positive or negative. Then, the arbitrary value of y used MAY determine whether the solutions proposed is well defined or not, but that does not ADD more solutions, it can potentially subtract solutions instead.

For example, when you start with \(f(x)= \frac{2x+1}{x-1}\), and you solve for x this: \(y = \frac{2x+1}{x-1}\), you will get to

\(x = \frac{y+1}{y-2}\)

which means that for a given \(y\) you have AT MOST one solution. Why one solution at most? Because when y = 2 there is actually no solution, and for any other y, there is one solution. This works great to show that the function passes the horizontal line test.

Example: Passing the HLT

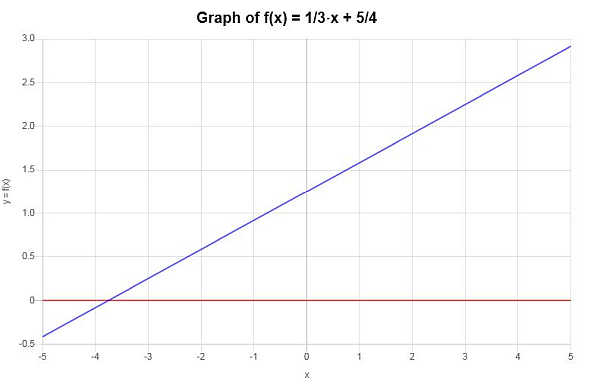
Does the following function pass the HLT: \(f(x) = \frac{1}{3} x + \frac{5}{4}\) ?

Solution:

The function that has been provided is:

\[f\left(x\right) = \frac13x+\frac54\]

Then, in order to assess whether or not the given function passes the Horizontal Line Test, we need to solve for \(x\) and determine whether there is no solution, one solution, or multiple solutions. The starting equation is

\[y=\frac{1}{3}x+\frac{5}{4}\]

Solving the Linear Equation

Putting \(x\) on the left hand side and \(y\) and the constant on the right hand side we get

\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]

Now, solving for \(x\), by dividing both sides of the equation by \(-\frac{1}{3}\), the following is obtained

\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]

and simplifying we finally get the following

\[\displaystyle x=3y-\frac{15}{4}\]

Therefore, the solving for \(x\) for given linear equation leads to \(x = 3y-\frac{15}{4}\).

We find that since when solving for \(x\) we find a solution and it is only one solution, the given function passes the Horizontal Line Test.

The Horizontal Line Test Results

Based on the work shown above, it can be concluded that the given function passes the Horizontal Line Test.

Graphically, the situation is be depicted as follows:

Example: Is this function One-to-One?

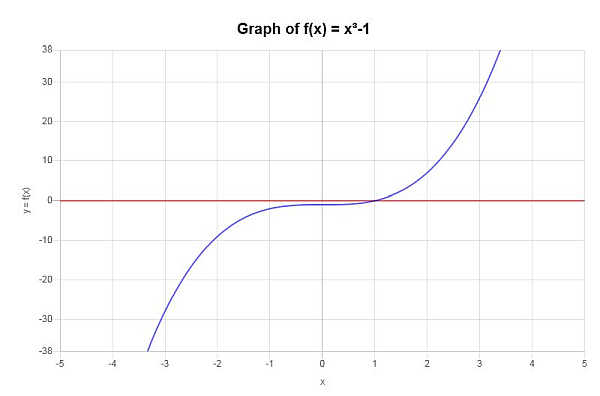
Using the horizontal line test, indicate whether the following function is one-to-one: \(f(x) = x^3 - 1\)

Solution: In order to assess whether or not the given function passes the Horizontal Line Test, we need to solve the equation \(y = x^3 - 1\) for \(x\) and determine whether there is no solution, one solution, or multiple solutions.

Initial Step: In this case, we first need to simplify the given equation, and in order to do so, we conduct the following simplification steps:

Then, we obtain the solutions:

\[x_1=\left(y+1\right)^{\frac{1}{3}} \] \[x_2=\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}-1\right) \] \[x_3=-\frac{1}{2}\left(y+1\right)^{\frac{1}{3}}\left(i\sqrt{3}+1\right) \]

Out of these solutions, we have only one real solution, which is \(x_1=\left(y+1\right)^{\frac{1}{3}}\). Therefore, and since when solving for \(x\) we find a solution and it is only one real solution, the given function passes the Horizontal Line Test.

Graphically we get:

More function calculators

Dealing with functions is something that will inevitably do when taking an Algebra or Calculus course. Using a function calculator can help you simplify a function or graph a function, tasks that are crucial in your undergraduate skillset.

The concept of the horizontal line test and functions that are one-to-one is very tight, and that will come in handy when finding the inverse of a function, something that is very common is basic math courses.

From the Calculus side of things, you also often times may get involved with dealing with derivative rules and the calculation of derivatives, but that happens after a complete Algebra 101 class, when the fundamentals are covered first, before getting to deal with derivatives or integrals