The Absolute Value
The absolute value of a number corresponds to its magnitude, without considering its sign, if it has it. Geometrically, it corresponds to the distance of a point \(x\) to the origin \(0\), on the real line
Mathematically the absolute value of a number \(x\) is represented as \(|x|\).
Due to the geometric nature of its interpretation, the absolute value is extensively used in algebra and other math branches, and it turns out that it is very easy to compute the absolute value of a given number: all you have to do is to drop the sign, if there is a sign.
EXAMPLE 1
Calculate the absolute value of \(-8\).
ANSWER:
As we mentioned above, the absolute value of a number is its magnitude, without taking the sign into account. In this case, by dropping the sign, we realize that the absolute value of \(-8\) is \(8\). Mathematically, we write \(|-8| = 8\).
EXAMPLE 2
Calculate the absolute value of \(4\).
ANSWER:
We know that the absolute value of a number is its magnitude, without taking the sign into account. In this case, there is not a sign to drop, so get that the absolute value of \(4\) is simply \(4\). So, mathematically, we write \(|4| = 4\).
EXAMPLE 3
What is the absolute value of -5.
ANSWER:
As we have seen before, absolute value of a number is the number without the sign (if it has it). In this case, there is a sign to drop, and find that the absolute value of -5 is 5. Mathematically, we write \(|-5| = 5\).
Mathematical Definition of Absolute Value
This idea of "dropping the sign" would be enough if all we do is to compute absolute value of numbers. But actually we do more things, which are a bit more complicated, such as absolute value equations and inequalities.
Mathematically, the formal definition of \(|x|\) is given below.
\[|x|=\left\{ \begin{array}{cc} x\text{ } & \,\,\,\text{for }x\ge 0 \\ \\ -x & \,\,\text{ for }x<0 \\ \end{array} \right.\]Without panicking, let us analyze the above definition. It is simply saying: "Check the given number \(x\). If \(x\) greater than or equal zero, then the absolute value of the number will be the number itself. Otherwise, if the given number \(x\) is negative, the absolute value of the number is \(-x\), which would correspond to multiplying the originally given number by \(-1\).
So then, in the case of \(-8\), this number of negative, so the absolute value is obtained by multiplying it by \(-1\), so we get \(|-8| = (-1) \times (-8) = 8\). That is all.
Now, this definition may look like an overkill. After all, why not to stick with the "drop the sign" method? There is a reason for that, and it is simply because this way of defining the absolute value help us to handle harder situations involving absolute value.
For example, if I ask you to solve the following inequality: \(|x^2-4x+10| \ge 0\), would you be able to just "drop the sign" to reduce it? Not quite. Do not worry, we discuss inequalities involving absolute values in another tutorial.
Only wanted to point out why we take the work to make a formal definition of the absolute value, and it because at some point we will need it, when we handle more complicated operations involving absolute values.
How to compute the Absolute Value
Following these steps to safely compute the absolute value of a given number.
- Assess if the given number is valid. If not, you cannot compute the absolute value
- If the number is valid, check if it comes with a sign, this is, if it is positive or negative
- If the number is positive (or zero), the absolute value of the number is the same number
- If the number is negative, multiply the expression by -1 to get your your absolute value
Properties of the Absolute Value
These are the main properties:
1) \(|0| = 0\)
2) \(|ab| = |a||b|\), for \(a\) and \(b\) real numbers
3) \(|a+b| \le |a|+|b|\), for \(a\) and \(b\) real numbers
The Fallacy of the Square Root of a square
Finally, I would like to give credit to the absolute value for a missing reference. Yes, it deserves credit. Indeed, often times we see in high school or even in college a muddy statement like:
\[\large \sqrt{x^2} = x\]with a statement saying that "the square root cancels the square". I am not going to say that is false, but I will say that it true when \(x\) is non-negative. The true statement would be
\[\large \sqrt{x^2} = |x|\]and there you have one of the stellar appearances of the absolute value. In time you will realize that it shows up more frequently than what you think.
More About the Absolute Value
The absolute value is a simple concept, and it is a really useful one, because it has a clear geometric interpretation in the real line: it represents the distance of any point to the origin.
Although it is simple to compute it for a number, there are more complicated operations that involve absolute values, such as the absolute value equations and inequalities. Those require a clear strategy to be solved, otherwise you can get stumped.
How to Find an Absolute Value?
Typically is not that hard to find the absolute value of a given number: all you have to do is to get the magnitude of the number, without considering the sign. In other words, and to make it simple, just see if there is a sign and drop it.
The procedure is less evident when you are computing the absolute value of an algebraic expression, in which case you need to first reduce the expression to a number, and then drop any sign if it has it.
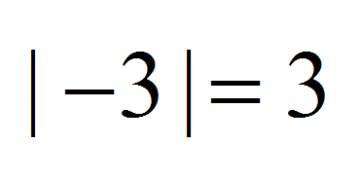
Applications of the Absolute Value
Using the absolute value goes beyond simply computing the absolute value of numbers. The absolute value has some intrinsic properties that make it an invaluable analytical tool.
For example, absolute value appears frequently in many situations, like for example for \(\sqrt{x^2} = |x|\), which is usually taken for granted, as most people will use \(\sqrt{x^2} = x\), which incorrect when \(x\) is negative.
The absolute value also appears in geometry (because the absolute value of a difference represents the distance between two points), in integration and for when we need to solve absolute value inequalities .
Also, you can use this absolute value calculator to practice the concepts learned in this tutorial. Or for more general calculations, you can use this algebraic expression calculator .
