In this tutorial we will cover the concept of horizontal asymptote and its most important applications. We will try to avoid any overly technical explanations, but some touches of Calculus will be used.

Mostly, the important part to get out of this tutorial is a strong geometric intuition about horizontal asymptotes. Let's begin!

What is an horizontal asymptote

A Horizontal Asymptote is an upper bound, which you can imagine as a horizontal line that sets a limit for the behavior of the graph of a given function.

This means that the graph of the function $f(x)$ sort of approaches to this horizontal line, as the value of $x$ increases.

How do you find the horizontal asymptote?

Understanding this limiting horizontal behavior of functions that exhibit this characteristic can prove to be very useful to find horizontal asymptotes.

Indeed, on certain circumstances, this limiting behavior looks pretty like that of a horizontal line for large values of $x$. See the function below for example.

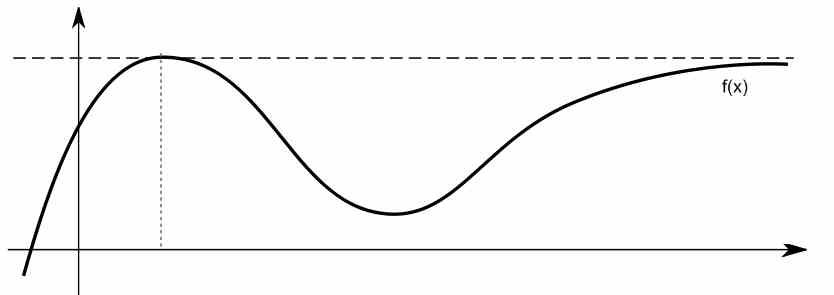
How do you find the horizontal asymptote of a function using limits?

In order to make the definition clear, a horizontal line $y = h$ is a horizontal asymptote of the function $f(x)$ if

if the above limit exists and it is finite. For those who haven't yet gone through a calculus class, horizontal line $y = h$ is a horizontal asymptote of the function $f(x)$ when $h$ is the limit of $f(x)$ as $x$ approaches to infinity. What does being a "limit" means? It means that for values sufficiently large of $x$, the value of $f(x)$ will be as close to $h$ as we predetermine. Fancy, right?

What is the formula for the horizontal asymptote?

In order to find the formula for the horizontal asymptote, we first need to find the corresponding limit. Assume that you have

In that case, we will say that the horizonal asymptote is $h$, and the formula for the horizontal asymptote is $y = h$. In other words, the horizontal asymptote is simple is horizontal line, this is a line with slope zero.

This gives the meaning to what a horizontal asymptote means in terms of limits: the limit found corresponds to define the horizontal line that is called the horizontal asymptote.

EXAMPLE 1

Find a horizontal asymptote for the function

ANSWER:

In order to find the horizontal asymptote, we need to find the limit of the function $f(x)$ as $x$ approaches to infinity. If you are not familiar with Calculus, you should first try to evaluate the function at a very large value of $x$.

For example, let's say that $x = 1,000,000$. Let us plug this number in the function:

which is darn close to 1. So then one should suspect that the limit is 1. In fact, it turns out that when $x$ is large, the value of $x^2$ is so large with respect to 1, that $x^2$ is very similar to $x^2 + 1$ at least in relative terms. So we have, by dividing numerator and denominator by $x^2$:

because $\frac{1}{x^2}$ approaches to 0 as $x$ approaches to infinity. Therefore, it is not hard to prove, or be convinced that

which means that the horizontal asymptote is $y = 1$. Now, be careful with your answer if you are answering a test or homework. Some people will say "the horizontal asymptote is 1", which is wrong.

Technically, the horizontal asymptote is the function $y = 1$, and NOT the number 1. The horizontal asymptote is a function that is constant, which is not the same as a number. Just saying, because there are some picky graders out there.

EXAMPLE 2

Find a horizontal asymptote, if it exists for the function

ANSWER:

By dividing numerator and denominator by $x^2$:

But wait! The trick did not work here? Yes it did. Notice that the denominator will become very close to 1 as $x$ becomes very large, and the numerator will become very large.

It is not hard to believe that $f(x)$ converges to infinity, so that there is not a horizontal asymptote. Any time we see a function that is unbounded, like it is the case for $f(x)$ in this example, we won't have a horizontal asymptote.

Horizontal Asymptote or Horizontal Asymptotes?

Technically there could be two horizontal asymptotes, one to the left and one to the right. The left horizontal asymptote is $y = h_L$ if

Similarly, the right horizontal asymptote is $y = h_R$ if

in case that any of the above limits exists, and are finite. It can happen that a function has two horizontal asymptotes, it has only one horizontal asymptote, or it has none.

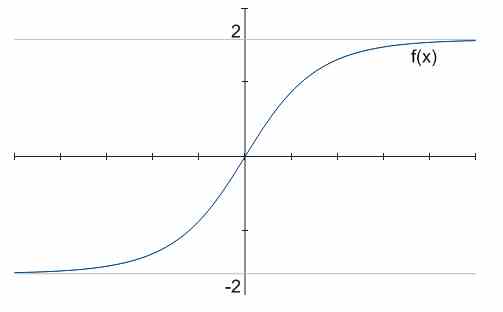
For example, in the graph above, there are two horizontal asymptotes, $y = -2$ and $y = 2$.

What is the rule for finding horizontal asymptote?

There are no general rules that will work for all cases. In the general case we need to compute the limit as $x$ approaches to $-\infty$, and the limit as $x$ approaches to $+\infty$.

If any of those limits exist and are finite, we will have the horizontal asymptotes.

One specific rule can be devised for the case that the given function $f(x)$ is the quotient of two polynomials. If that is case, let us assume that $m$ is the order of the polynomial in the numerator, and $n$ is the order of the polynomial in the denominator. Then we have the following cases:

Case 1: If $m < n$, then the horizontal asymptote is $y = 0$.

Case 2: If $m = n$, and $a$ is the leading coefficient for the polynomial in the numerator, and $b$ is the leading coefficient for the polynomial in the denominator, then the horizontal asymptote is $\displaystyle y = \frac{a}{b}$.

Case 3: If $m > n$, then there is no horizontal asymptote.

EXAMPLE 2

Find, if exists, the horizontal asymptote of the function

ANSWER:

The function consists of the quotient of two polynomials. The polynomial in the numerator is $3x^2+2x-1$, which is a polynomial of order 2, so then $m = 2$, and leading coefficients 3.

The polynomial in the denominator is $2x^2 -x+2$, which is a polynomial of order 2, so then $n = 2$, and leading constant 2. You can use our polynomial calculator to conduct this division showing all the steps.

Hence, since in this case $m = n$, there is a horizontal asymptote, and it is the quotient of the leading coefficients, so then in this case, the horizontal asymptote is