The concept of function is extremely important and it is absolutely omnipresent in Math. That is why we need to give it a good brush up, before attempting to understand some of the goodies that will come afterwards when go deeper into Calculus topics, such as differentiation and integration.

WHAT IS A SET?

The first element we need to understand is the concept of a set . A set is simply a collection of elements. So then, a set is quite simply defined by way of knowing which elements belong to the set and which element don’t. It appears to be a super simple task and the theory of set should be simply reduced to having unambiguous rules for determining which elements belong to a set.

For example, let us define the set of even number, and we call it $E$. Why is it even a set? Because it has an unambiguous rule to determine which elements belong to $E$: A real number $x$ belongs to $E$ if it is divisible by 2. The rule works unambiguously for every single real number determining whether or not it belongs to $E$. Why I say “unambiguously” and keep repeating. Because it is important. Unambiguously means that the there is no way to conclude that a given $x$ both belong and doesn’t belong to $E$. Unfortunately things sometimes go beyond our imagination. Contrary to our intuition, a set definable with a simple rule of belonging can lead to an ambiguous (contradictory) belonging classification, as shown by Bertrand Russell in his famous paradox. Russell showed that a more careful definition of what a set is should be used.

For all practical purposes, we will think of a set as a collection of elements, definable by a rule of belonging .

WHAT IS THE PRODUCT OF TWO SETS?

Let $A$ and $B$ be sets, in the context of the definition given above. The product $A\times B$ of two sets is another set, which is defined as the set of all possible ordered pairs of the form $\left( a, b \right)$, where $a$ belongs to $A$ and $b$ belongs to $B$. So then, $A\times B$ is a set, and its elements are ordered pairs of the form $\left( a ,b \right)$. Don’t let that notation to impress you. When I say “ordered pairs of the form $\left( a, b \right)$”, the symbol $\left( a, b \right)$is a made up symbol, to indicate an element that is composed of two entities $a$ and $b$, and identify the first element as being $a$, and the second element as being $b$. That’s it. Instead of $\left( a,b \right)$, we could have chosen the symbol $a\_b$, and it would have worked alright.

You will have to forgive me, but I have to write the mathematical definition of the product of two sets (we can multiply sets, too….what did you think, we would stop with numbers only, uh?):

$A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}$

The reason why I write the definition is for you to look at it and recognize how using a very compact notation we are saying exactly the same as the way I defined it with words in the paragraph above. I hope you will loosen up some fear for reading math statements. Mathematicians could be funky people sometimes, but they do find good, unambiguous and compact notations. And consequently, Math language is SUPER easy to read. Right? Right? Please tell me I’m right…

A side note, for historical reasons, the product of two sets $A\times B$ is normally referred as a Cartesian product .

NOW, THE DEFINITION OF A FUNCTION (FINALLY)

Ok, I lied, there is one more step before defining what a function is. We need to define the concept of relation . What is a relation? Beyond its common use as an English word, a relation is simply a subset of a Cartesian product. ANY subset of a Cartesian product is a relation. So then if $A$ and $B$ are sets, a set $R$ is a relation if $R\subseteq A\times B$. Since any set can be considered as a subset of itself, then all Cartesian products are relations themselves.

Put it on a frame:

A relation is a set that is a subset of a Cartesian product

Let us get more graphical. Consider the set $A=\left[ 0,1 \right]$ (which is all the real numbers that are greater than or equal to 0, and they are also less than or equal to 1). What is the Cartesian product $A\times A$? Let’s parrot what we just learned. The Cartesian product $A\times A$ is $\left[ 0,1 \right]\times \left[ 0,1 \right]$in this case is the set of all pairs$\left( x, y \right)$, where both $x$ and $y$ belong to $\left[ 0,1 \right]$. Cartesian products are typically easy to graph. Look at the shaded region below:

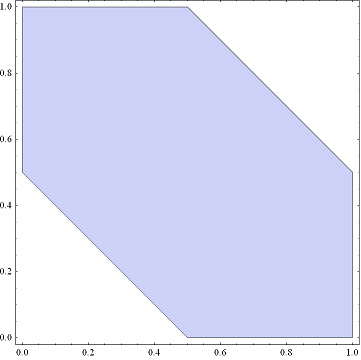
Now, what would make a relation? We can “carve” out all we want the shaded region above, and what is left is a relation in $\left[ 0,1 \right]\times \left[ 0,1 \right]$. For example, we can cut the “corners” out to get the following sub-region:

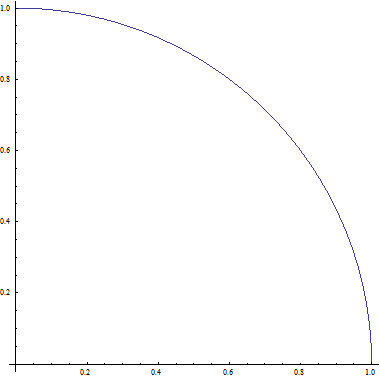
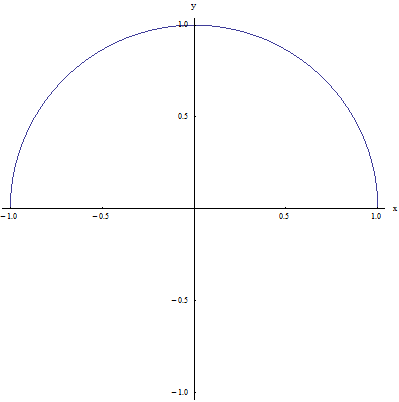
The region (set) above is a relation. Why? Because it is a subset of the Cartesian product $\left[ 0,1 \right]\times \left[ 0,1 \right]$. But we can carve out even more. How about carving out a quarter a circle? See the region below.

The region (set) above is a relation. Why? Again, because it is a subset of the Cartesian product $\left[ 0,1 \right]\times \left[ 0,1 \right]$.

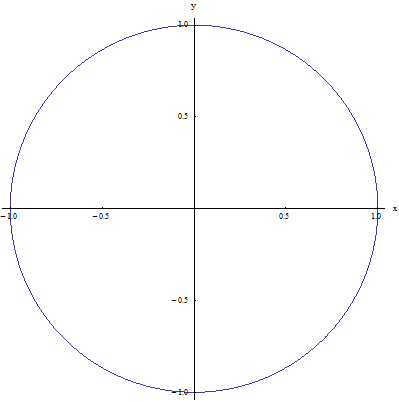
Now, let me give you an example of two relations in $\left[ -1,1 \right]\times \left[ -1,1 \right]$. Se the graphs below:

Relation 1

Relation 2

They are both obviously relations (because they are both contained in the Cartesian product $\left[ -1,1 \right]\times \left[ -1,1 \right]$, but they have one key difference: For Relation 1, for a given point x on $\left[ -1,1 \right]$, there two points ${{y}_{1}}$and ${{y}_{2}}$that that have the property that $\left( x,{{y}_{1}} \right)$ and $\left( x,{{y}_{2}} \right)$ belong to relation 1. For example for x = 0, there are two points ${{y}_{1}}=1$ and ${{y}_{2}}=-1$ such that $\left( 0,1 \right)$and$\left( 0,-1 \right)$ belong to relation 1. Now, for relation 2 that is not the case because, for example, for x = 0 it is only $y=1$ that makes the point $\left( 0,1 \right)$ belong to relation 1.

Finally we can define a function: A function $R$ is a set that is a relation and it also has the property that if the point $\left( x,y \right)$belongs to $R$, then there is no other point $\bar{y}$ different from $y$ that has the property that $\left( x,\bar{y} \right)$ belongs to $R$ as well. In other words, a function is a relation with the extra requirement that each $x$ in its domain is associated with only one $y$.

How do know how to differentiate between a function and a relation??

Gadgets! We use a little trick call the “Vertical Line Test”: We draw an imaginary vertical line, and we sweep around moving it left to right all the way, and making a mental map of where the vertical line intersects the relation.

• If at ANY point, the vertical line intersects the relation at MORE than one point, then the relation fails the vertical line test, and then the relation is not a function

• If at ANY point, the vertical line does not intersect the relation anywhere at MORE than one point, then the relation passes the vertical line test, and then the relation is a function

See the two examples below:

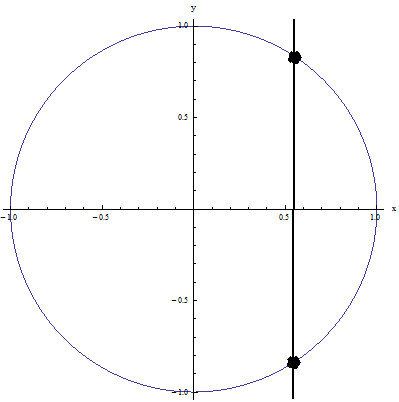
Example 1: It fails the vertical line test because the vertical line shown in the figure intersects the relation at more than one point: NOT A FUNCTION

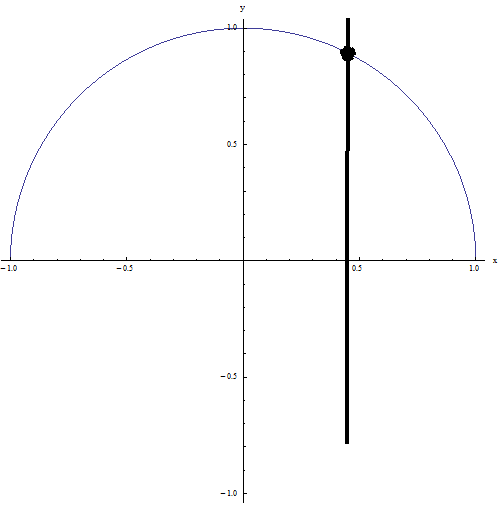
Example 2: It passes the vertical line test because no vertical line intersects the relation at more than one point: IT IS A FUNCTION!

There are many graphical applications that can be conducted with functions, including the calculation of horizontal asymptotes , vertical asymptotes, and slant asymptotes if applicable.