Equation of the Line in Standard Form Calculator
Instructions: Use this calculator to find the equation of the line in standard form, showing all the steps. For that, you need to provide information about the line you want to put into standard form.
You have a number of ways to do that. You can provide: (1) both the slope and the y-intercept, (2) you can provide any linear equation (ex: \(2x + \frac{1}{5}y = 3 + 2x\)), (3) you can provide the slope and a point the line passes through, or (4) you can provide two points where the line passes through.
More about this equation of line in standard form calculator
This equation of the line in standard form equation calculator will allow you to define an equation in one of four ways you prefer, and it will show you all of the steps required.
How to find the equation of a line? So the first thing, is to define a linear equation. For this purpose, you can either provide an equation directly, or otherwise, depending on the information you have available, you can provide:
(1) the slope and the y-intercept.
Or (2) the slope and one point where the line passes through,
or (3) you can provide two points where the line passes through.
What way will you use to define your equation will depend on what information you have available.
What is the format of a linear equation in standard form?
A linear equation is said to be in standard form if it has the following structure:
\[a x + by = c\]Then, your goal is to determine the standard form formula and find the constants a, b and c that determine it.
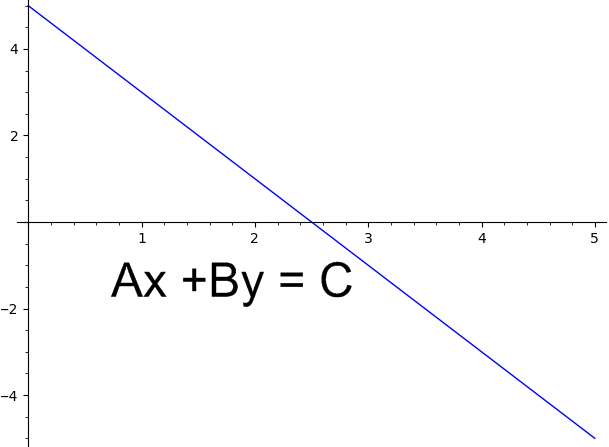
How do you solve standard form on a calculator?
With this calculator, all you have to do is provide information to define the equation, among the four different options.
Why is the standard form needed
Certain specific forms of an equation come from tradition, but usually because it is useful to use a specific form.
In the case of the standard form, it is practical to have it in the form \(a x + by = c\), because by plugging \(x=0\) it is easy to compute the y-intercept, and by plugging \(y=0\) it is easy to compute the x-intercept.
Also, the standard form is commonly used as the format of choice when solving simultaneous systems of linear equations.
Can this solver deal with fractional linear equations?
One of the neat things about this calculator is that all the coefficients you use to define the equation can be any generic numeric expression, which includes fractions.
In order to see an example of how this calculator deals with fractional linear equations, check the example below.
Example: Calculation of the equation of a line
Assume that you have a line that passes through the point \(\left( \frac{1}{3}, \frac{2}{3}\right)\) with slope \(m = \frac{1}{2}\). Find the standard form of the line.
Answer:
The information initially provided about the line is that the slope is \(\displaystyle m = \frac{1}{2}\) and the line passes through the point \(\displaystyle \left( \frac{1}{3}, \frac{2}{3}\right)\)
Hence, with the information we have, we can construct directly the point-slope form of the line, which is
\[\displaystyle y - y_1 = m \left(x - x_1\right)\]and then plugging the known values of \(\displaystyle m = \frac{1}{2}\) and \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, \frac{2}{3}\right)\), we get that
\[\displaystyle y-\frac{2}{3} = \frac{1}{2} \left(x-\frac{1}{3}\right)\]Now, we need to expand the right hand side of the equation by distributing the slope, so we get \[\displaystyle y = \frac{1}{2} x + \frac{1}{2} \left(-\frac{1}{3}\right) + \frac{2}{3}\]
and simplifying we get that \[\displaystyle y=\frac{1}{2}x+\frac{1}{2}\]
Passing the independent variable to the left hand side of the equation leads to the following standard form of the line:
\[\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\]Conclusion: Based on the data provided, we conclude that the equation of the line in standard form is \(\displaystyle -\frac{1}{2}x+y=\frac{1}{2}\).
Other useful calculators related to linear functions
Often times, you just want to have a quick look at how things look graphically, for which you could use this tool for graphing linear equations
Or you can also graph two linear equations and find the intersection of two lines, if it exists.
As a previous step, you may want to compute the slope first, so to you the slope-intercept form, for which you could use this slope of a line formula calculator.





