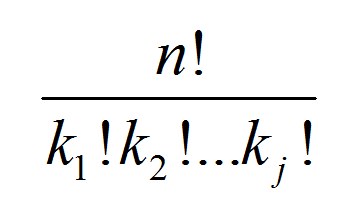The Multinomial Coefficients

The multinomial coefficient is widely used in Statistics, for example when computing probabilities with the hypergeometric distribution .

By definition, the hypergeometric coefficients are defined as:

\[ \displaystyle {N \choose k_1 k_2 ... k_j} = \frac{N!}{k_1! k_2! ... k_j!} \]

with \(k_1 + k_2 + ... + k_j = N\). By observing at the form above, the multinomial coefficient is clearly a generalization of the combinatorial coefficient , only that instead of two combinations, you have \(j\) combinations.

Other Applications

The multinomial coefficients are also useful for a multiple sum expansion that generalizes the Binomial Theorem , but instead of summing two values, we sum \(j\) values.

Question for you: Do you think that there is something similar as the Pascal Triangle for multinomial coefficients as there is for binomial coefficients?