Rational Functions

This rational function calculator will allow you to analyze the most relevant points of a rational function you provide, with all the steps shown. Typically, for most rational functions you can find intercepts, vertical asymptotes and its graph. Some specific rational functions will also have horizontal asymptotes.

The type of function you can provide is like 'f(x)=1/x - x', or something involving polynomials of higher degree like 'f(x) = (x^3-1)/(x^2+x)'

Once a valid rational function has been provided, you can click on the calculate button, and you will get all the steps shown for you.

One of the main attributes of a rational function is that you can mostly reduce the calculation to the problem of solving polynomial equations, which is one of the "simplest" types of equations you can solve.

What is a Rational Function

A rational function is a function that involves the quotient of two polynomials \(P(x)\) and \(Q(x)\), where the divisor \(Q(x)\) is not equal to the zero polynomial. So then, the rational function formula is

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

For example, the function

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

is a rational function, because it is precisely the quotient of two polynomials. But for example

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

is not rational because the divisor is not a polynomial. Observe that when we say that the divisor \(Q(x)\) is not equal to the zero polynomial, we are NOT saying that \(Q(x)\) cannot have zeros. For example, in this case of \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \), the divisor is \(Q(x) = x + 1\), which has a one zero, at \(x = -1\).

What we don't want is something like

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

because although in this case \(Q(x) = 0\) is technically a polynomial, it is the zero polynomial (which is zero everywhere).

Steps for calculating a Rational function

• Step 1: First, make sure you do have a rational function, for which you can identify the numerator P(x) and denominator Q(x)
• Step 2: If you don't find strictly the structure described above, you stop. You may need to group terms together via algebraic reductions.
• Step 3: You need to find the real zeros of P(x) and Q(x), if any. The conclusions found will be tightly related to the zeros of both P(x) and Q(x)
• Step 4: To find the y-intercept, you evaluate the function at zero, by computing f(0). The y-intercept will be well defined if x = 0 is not a zero of Q(x)
• Step 5: To find the x-intercepts, you get the zeros of P(x) that are not zeros of Q(x)
• Step 6: For finding vertical asymptotes, you need to find the zeros of Q(x) that are not zeros of P(x)
• Step 7: For finding horizontal asymptotes, you need to have that the degree of Q(x) is greater than or equal to the degree P(x)

Observe that as expected, analyzing a rational function depends on finding zeros of a polynomial, and then putting all the conclusions together. .

Notice that the domain of a rational function is the whole real line except for the zeros of the divisor Q(x). If there is a zero of Q(x) that is also a zero of P(x), then the discontinuity can be repaired. The range of a rational function will depend on the degrees of P(x) and Q(x).

Why using Rational Functions

Rational functions are used because they are natural extensions of polynomials. One can see them as the next step in complexity of a function. As we know, polynomials expressions are among the simplest functions we can find, but yet they are among the most useful as well.

Rational equations will typically appear in more advanced mixing problems, and yet, they are surprisingly simple to handle, provided that the polynomials involved are simple enough. We know how to solve quadratic equations, but for polynomials of degree 3 and higher things can be more hairy.

Are Polynomial Functions also Rational Functions

Yes, if P(x) is a polynomial, then P(x) is also rational, because we can write:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

and Q(x) = 1 is an actual polynomial. The other way around is not true: a rational function is not necessarily a polynomial. Why is that? Because naturally, unless Q(x) = 1, whenever you have \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), you won't have that all the terms will be free terms as required by the definition of a polynomial.

More formally, using Remainder Theorem, we have

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

where \(d(x)\) is a polynomial, but \frac{r(x)}{Q(x)} is not, because the degree of r(x) is lower than the degree of Q(x).

Example: Working with Rational Functions

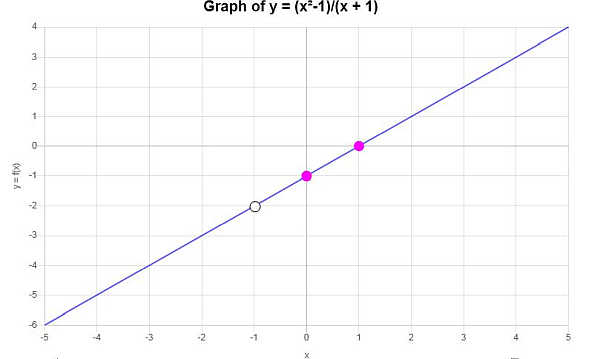
Find the intercepts and asymptotes and graph of : \(f(x) = \frac{x^2-1}{x+1}\)

Solution:

We have been provided with the following function:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

We need to find the intercepts and asymptotes, if any. After that, the graph of the function will be presented.

Let us find the zeros of the given function. We need to solve the following rational equation:

\[\frac{x^2-1}{x+1}=0\]

Observe that for \(x \ne -1\) we can simplify as:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Auxiliary Numerator Equation

Now we set the numerator equal to zero and find the solutions. Then, those roots that do not make the denominator equal to zero will be solutions to the rational equation.

The following needs to be solved to find the roots of the numerator: \(x^2-1=0\)

For a quadratic equation of the form \(a x^2 + bx + c = 0\), the roots are computed using the following formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In this case, we have that the equation we need to solve is \(\displaystyle x^2-1 = 0\), which implies that corresponding coefficients are:

\[a = 1\] \[b = 0\] \[c = -1\]

First, we will compute the discriminant to assess the nature of the roots. The discriminating is computed as:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Since in this case we get the discriminant is \(\Delta = \displaystyle 4 > 0\), which is positive, we know that the equation has two different real roots.

Now, plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

so then, we find that:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Auxiliary Denominator Equation

We need to find the roots of the denominator: \(x+1=0\)

Therefore, the solving for \(x\) for given linear equation leads to \(x=-1\).

Numerator and Denominator Zeros

Based on the analysis shown above, the real zeros of the numerator of the given rational function are \( x_{ 1} = -1\) and \( x_{ 2} = 1\).

Also it is found that the denominator has one real zero, which is \( x_{ 1} = -1\).

Finding X-Intercepts

Based on the zeros of the numerator that are not zeros of the denominator, we find that there is one x-intercept, which is \(\left(1, 0\right)\).

Finding Y-Intercepts

By evaluating the function provided at \(x = 0\), we find that:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

so then the y-intercept is \( \left(0, -1\right)\).

Vertical Asymptotes

After analyzing the zeros, it is concluded that the function does not have vertical asymptotes.

Horizontal Asymptotes

Notice that the degree of the numerator is \(2\) and the degree of the denominator is \(1\), and then, since the degree of the polynomial in the numerator exceeds that of the one in the denominator, we conclude that there is no horizontal asymptote.

The following graph is obtained:

Example: Horizontal asymptotes

Does this rational function have a horizontal asymptote: \(f(x) = \frac{x^2-1}{x^2+1}\)?

Solution: Clearly in this case, the function consists of the quotient of two polynomials, and they both have a degree equal to 2. This is, they have the same degree and therefore, there is a horizontal asymptote.

We can see this using limits too:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

which implies that the horizontal asymptote is \(y = 1\). This concludes the calculation.

Useful function calculators

Functions are fundamental mathematical objects, which encapsulate the relationship between different variables. Using a function calculator can help you systematically deal with functions that may be too complicated to handle by hand.

Graphing rational functions is one of the most common toy examples that students learn in Algebra and Calculus, and though perhaps rational functions do not show up per se all that often in applications, the analytical skills required to deal with the can prove invaluable

The same goes for solving rational equations, where the principles of manipulating algebraic expressions and reduce them to their lower terms will be extremely powerful for the achievement of more advanced skills.

Now, if we are talking about function, we cannot forget the calculation of the derivative of a function, integration and other more advanced infinitesimal techniques.