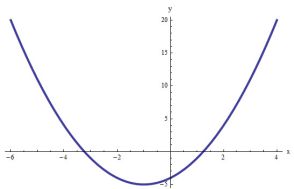
Quadratic Graph
Instructions: Use this Quadratic Graph calculator to create the graph of any quadratic function you provide, showing all the steps. Please type in the quadratic function you want to graph in the form box below.
More on this quadratic graph generator
This quadratic graph calculator will allow you to generate the graph for any quadratic function you provide. It can be any valid quadratic function, for example, x^2 - 3x + 1/2, but you can also provide a quadratic function that is not simplified, like x^2 - 3x - 4 - 1/2 x^2 - 1/5, provided that is a valid quadratic function.
Once you provide a valid quadratic expression, you can click on the "Calculate" button, and the graph of the function will be generated, showing you the steps of the calculation of the vertex of the parabola and the axis of symmetry as well .
Quadratic functions have a predominant role is basic Algebra, as they are frequently used in the context the solution to quadratic equations and application problems. They are essentially basic polynomials, that have a lot of interesting properties.
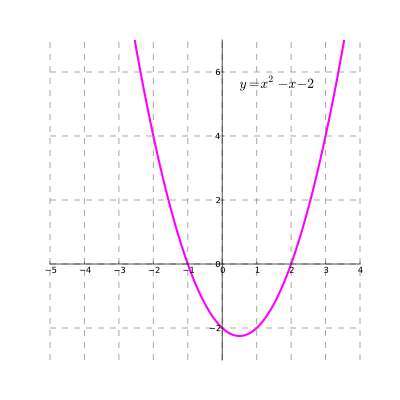
How to graph quadratics?
Doing a quadratic graph is simple, in the sense that you know that ALL quadratic functions will have the shape of a parabola. But yet there are infinite parabolas. We need to know a bit more in order to identify THE precise parabola that represents a given quadratic function.
Steps to find a quadratic function graph
- Step 1: Identify clearly the given quadratic function, and simplify if necessary
- Step 2: After simplifying, identify the function in the form f(x) = ax² + bx + c. Notice that a cannot be zero
- Step 3: If a > 0, you know the graph will be a parabola that opens upward, whereas if a < 0, you know the graph will be a parabola that opens downward
- Step 4: The axis of symmetry is at x* = -b/(2a), which tells you the 'center' of the parabola
- Step 5: Notice x* = -b/(2a) is the x-coordinate of the vertex of the parabola, and y* = f(x*) = a(x*)² + b(x*) + c is the y-coordinate of the vertex
That should be enough to have clear idea about the corresponding quadratic graph. A further step would be to plot some points on the graph, by choosing different points in the x-axis and finding their corresponding image through the function, so to the aid the process of finding the graph of the function.
The Quadratic Formula
Is the quadratic formula related to the graph of a quadratic function? You bet! Geometrically speaking, the when solving the quadratic equation
\[a x^2 + bx + c = 0 \]you get the roots of the quadratic equation, and when the roots are real, they represent the points where the parabola crosses the x-axis.
A special case occurs when the roots are complex, in which case the parabola won't cross the x-axis.
Types of quadratic graphs
As we mentioned before, ALL univariate quadratic functions will be represented by parabolas, but depending on whether a > 0 or a < 0, the parabolas will open up or down respectively.
Another distinction of the types of parabolas could be for the ones that are "centered" (this is, the vertex is a the origin), and those that are not.
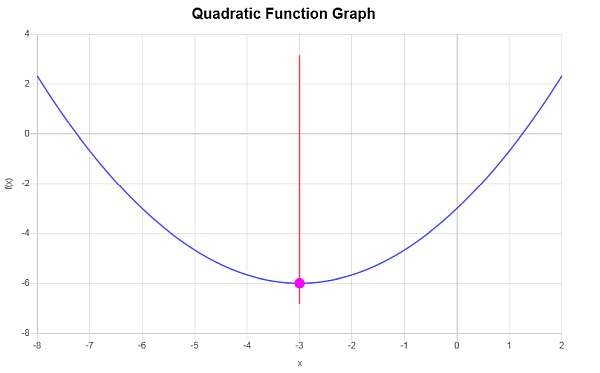
Example: Quadratic Graph
Construct the graph of : \(f(x) = \frac{1}{3}x^2 +2x - 3\)
Solution:
We need to graph the provided quadratic function \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\). Also, the coordinates of the vertex will be computed.
For a quadratic function of the form \(f(x) = a x^2 + bx + c\), the x-coordinate of the vertex is computed using the following formula:
\[x_V = \displaystyle -\frac{b}{2a}\]In this case, we have that the function for which we need to find the vertex for is \(f(x) = \displaystyle \frac{1}{3}x^2+2x-3\), which implies that corresponding coefficients are:
\[a = \frac{1}{3}\] \[b = 2\] \[c = -3\]Plugging the known values of \(a\) and \(b\) into the formula for the x-coordinate of the vertex, we get:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{2}{2 \cdot \frac{1}{3}} = -3\]Now, we need to plug the value of \(x_V = \displaystyle -3\) into the quadratic function, so we get:
\[y_V = f(x_V)\] \[ = \frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=\frac{1}{3}\cdot \left(-3\right)^2+2\cdot \left(-3\right)-3=9\cdot\frac{1}{3}-6-3=3-6-3=-6\]Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -3\), and the y-coordinate of the vertex is \(y_V = \displaystyle -6\). This indicates that the point that represents the vertex is \( \displaystyle \left(-3, -6\right)\).
The following is obtained graphically:
Example: Quadratic Graph
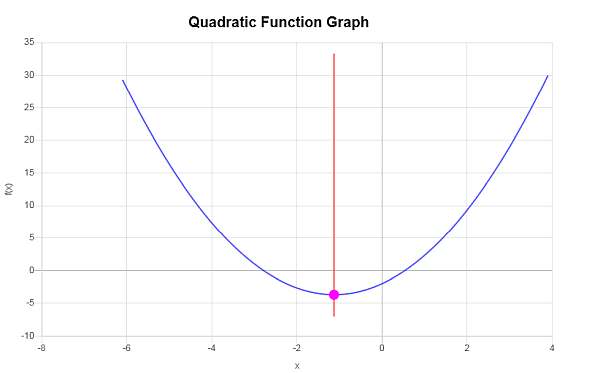
Graph: \(f(x) = \frac{4}{3}x^2 +3x - 2\), what type of quadratic graph is this?
Solution:In this case, we have that the function for which we need to find the vertex for is \(f(x) = \displaystyle \frac{4}{3}x^2+3x-2\), which implies that corresponding coefficients are:
\[a = \frac{4}{3}\] \[b = 3\] \[c = -2\]Plugging the known values of \(a\) and \(b\) into the formula for the x-coordinate of the vertex, we get:
\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot \frac{4}{3}} = -\frac{9}{8}\]Now, we need to plug the value of \(x_V = \displaystyle -\frac{9}{8}\) into the quadratic function, so we get:
\[y_V = f(x_V)\] \[ = \frac{4}{3}\cdot \left(-\frac{9}{8}\right)^2+3\cdot \left(-\frac{9}{8}\right)-2=\frac{4}{3}\cdot\frac{81}{64}+3\cdot \left(-\frac{9}{8}\right)-2=\frac{27}{16}-\frac{27}{8}-2=-\frac{59}{16}\]Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -\frac{9}{8}\), and the y-coordinate of the vertex is \(y_V = \displaystyle -\frac{59}{16}\). This indicates that the point that represents the vertex is \( \displaystyle \left(-\frac{9}{8}, -\frac{59}{16}\right)\).
The following is obtained graphically:
More quadratic calculators
Most all applications in basic Algebra are based on solving some sort of quadratic equation, so it has a strong pedagogical purpose to learn about it.
The quadratic formula is one of the most notorious teachable objects in Math. It is not that cubic or quartic equations don't exist, it is that quadratic equations are the ones we can easily explain.