This Vertex Formula Calculator

This calculator will allow to apply the vertex formula for a given quadratic function you provide. This quadratic function needs to be a valid one such as 2x^2 + 3x + 1/3, or it may come unsimplified such as 2x^2 - x + 5 - 3/4 x^2 +1/3, etc. Any valid valid quadratic function will do.

Once you provide a valid quadratic function, you need to click the "Calculate" button, and and the steps of the application of the vertex formula will be shown, with the steps followed to compute the vertex of the parabola.

Quadratic functions are really important in applications in Algebra and Calculus, and the vertex of a quadratic function is very interpretable.

What is the vertex formula?

First, we assume we start with a quadratic function, and we have simplified it to:

\[ f(x) = ax^2 + bx + c \]

Then, the vertex formula for the x-coordinate of the vertex is:

\[ x_V = \displaystyle -\frac{b}{2a}\]

How to apply the vertex formula?

• Step 1: Identify the quadratic function in its simplified form. You need to have something like f(x) = ax²+ bx + c
• Step 2: From the quadratic formula, you need to clearly identify what a and b are
• Step 3: From the a and b you identified, plug them into the formula xv = -b/2a

Notice that if a = 0, then the formula will be undefined, but in this case a won't be zero, since we have a quadratic function, and the term that multiplies x² cannot be zero in order to be a valid quadratic function.

How are the vertex and vertex form related?

They are tightly related. Indeed, if when you have a quadratic expression in vertex form, such as \(y = a(x-h)^2 + k\), then the vertex is immediately identified as having coordinates \((h, k)\).

So, in simple terms, the vertex form (also known as standard form), corresponding to centering the coordinates around the vertex.

Why is it important to find the vertex?

The vertex has a very important property, which is the point where the quadratic function reaches is minimum (when it opens upward when a > 0) or it is the point where the quadratic function reaches is maximum (when it opens downward when a > 0).

So then, when finding the vertex we are already getting the extreme point of the quadratic function, and also you can directly find the vertex form of the given quadratic expression.

Example: Calculate vertex

Calculate the vertex for the following quadratic function: \(f(x) = 3x^2+3x+2\)

Solution: We need to find the coordinates of the vertex of the quadratic function \(f(x) = \displaystyle 3x^2+3x+2\).

For a quadratic function of the form \(f(x) = a x^2 + bx + c\), the x-coordinate of the vertex is computed using the following formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In this case, we have that the function for which we need to find the vertex for is \(f(x) = \displaystyle 3x^2+3x+2\), which implies that corresponding coefficients are:

\[a = 3\] \[b = 3\] \[c = 2\]

Plugging the known values of \(a\) and \(b\) into the formula for the x-coordinate of the vertex, we get:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 3} = -\frac{1}{2}\]

Now, we need to plug the value of \(x_V = \displaystyle -\frac{1}{2}\) into the quadratic function, so we get:

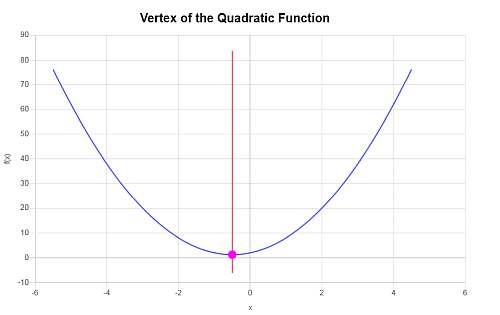
\[y_V = f(x_V)\] \[ = 3\cdot \left(-\frac{1}{2}\right)^2+3\cdot \left(-\frac{1}{2}\right)+2=3\cdot\frac{1}{4}+3\cdot \left(-\frac{1}{2}\right)+2=\frac{3}{4}-\frac{3}{2}+2=\frac{5}{4}\]

Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -\frac{1}{2}\), and the y-coordinate of the vertex is \(y_V = \displaystyle \frac{5}{4}\). This, the point that represents the vertex is \( \displaystyle \left(-\frac{1}{2}, \frac{5}{4}\right)\).

The following is obtained graphically:

Example: Vertex formula application

Use the vertex formula to calculate the coordinates of the vertex associated with the function \(f(x) = x^2 + 4x - \frac{3}{4}\)

Solution: Again, we use the following formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

Since \(f(x) = \displaystyle x^2+4x-\frac{3}{4}\), which implies that corresponding coefficients are:

\[a = 1\] \[b = 4\] \[c = -\frac{3}{4}\]

Plugging the known values of \(a\) and \(b\) into the formula for the x-coordinate of the vertex, we get:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{4}{2 \cdot 1} = -2\]

Now, we need to plug the value of \(x_V = \displaystyle -2\) into the quadratic function, so we get:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=1\cdot \left(-2\right)^2+4\cdot \left(-2\right)-\frac{3}{4}=-2^2+4\cdot \left(-2\right)-\frac{3}{4}=4-8-\frac{3}{4}=-4-\frac{3}{4}=-\frac{19}{4}\]

Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -2\), and the y-coordinate of the vertex is \(y_V = \displaystyle -\frac{19}{4}\). This, the point that represents the vertex is \( \displaystyle \left(-2, -\frac{19}{4}\right)\).

This concludes the calculation.

Example: Vertex application

Find the extreme point of the function \(f(x) = -2x^2 - 3x + 5\). Is this extreme point a minimum or maximum point?

Solution: We need to find the coordinates of the vertex of the quadratic function \(f(x) = \displaystyle -2x^2-3x+5\).

We use the following formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In this case, we have that the function for which we need to find the vertex is \(f(x) = \displaystyle -2x^2-3x+5\), so then:

\[a = -2\] \[b = -3\]

This means that:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{-3}{2 \cdot -2} = -\frac{3}{4}\]

Now, we need to plug the value of \(x_V = \displaystyle -\frac{3}{4}\) into the quadratic function, so we get:

\[y_V = f(x_V)\] \[ = \left(-2\right)\cdot \left(-\frac{3}{4}\right)^2-3\cdot \left(-\frac{3}{4}\right)+5=\left(-2\right)\cdot\frac{9}{16}-3\cdot \left(-\frac{3}{4}\right)+5 =-\frac{9}{8}+\frac{9}{4}+5=\frac{49}{8}\]

Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -\frac{3}{4}\), and the y-coordinate of the vertex is \(y_V = \displaystyle \frac{49}{8}\). This, the point that represents the vertex is \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\).

Notice that \(a = -2 < 0\), so then the parabola opens downward, and the point \( \displaystyle \left(-\frac{3}{4}, \frac{49}{8}\right)\) corresponds to a maximum point. This is, the quadratic function \(f(x) = \displaystyle -2x^2-3x+5\) reaches a maximum of \( \displaystyle \frac{49}{8}\) at \( x = -\frac{3}{4}\)

More quadratic calculators

Lots can be done with quadratic functions. You can compute the roots of a quadratic equation, you can find the axis of symmetry of a quadratic function, and so on and so forth.

Applying the vertex formula is tightly linked to applying the quadratic formula and the axis of symmetry.