Learn more about this Y-intercept calculator with steps.

The y-intercept of a line is the point where the line crosses the \(y\)-axis, and it is a very relevant point in many contexts.

In order to use this calculator you have to use the following steps:

1. Select one way of defining the line. You can actually provide an equation of the line , provide two points of the line, or one point in the line and the slope
2. Make sure you choose at least one of the methods and provide the info required for the option selected
3. Click on "Calculate"

How do you calculate the y-intercept?

The way you compute the y-intercept will depend on how you have specified the line. Often times, you can eyeball the graph of the line and more or less estimate where it crosses the y-axis, which is the finding the y-intercept on the graph method .

That way you can then get an idea at least of the approximate value of the y-intercept

How do you find y-intercept with the slope?

The ideal way, though, it is calculate the y-intercept algebraically. For example, when you have the equation in slope intercept form, using the line formula.

\[y = mx + n\]

you already know that the y-intercept is \(n\). Why? because \(y\), as a function of \(x\) is \(y = mx + n\). Then, when x = 0, we get \(y = n\), and we know \(x = 0\) is the point where the graph crosses the y-axis

Is the y-intercept a number or a pair (x, y)?

It depends a bit on the convention that you use. If the y value at which the line crosses the y-axis is \(y_{intercept}\), then the most commonly used way is that the y-intercept is the pair \((0, y_{intercept})\).

Though, if you say that the y-intercept is just \(y_{intercept}\), that is also correct, only that some instructors will ask you to write the y-intercept as an ordered pair.

But the x-coordinate of the y-intercept is ALWAYS 0, so some people find it redundant to write the full pair.

Can I get the Y-intercept calculator from two points?

Yes. In that case, you need to first use the two points to find the slope , using the following formula

\[m = \frac{y_2 - y_1}{x_2 - x_1} \]

Once you have the slope, you can construct the point-slope form using

\[y - y_1= m (x -x_1)\]

And then solving for \(y\) you will get the slope-intercept form , which gives you the y-intercept directly

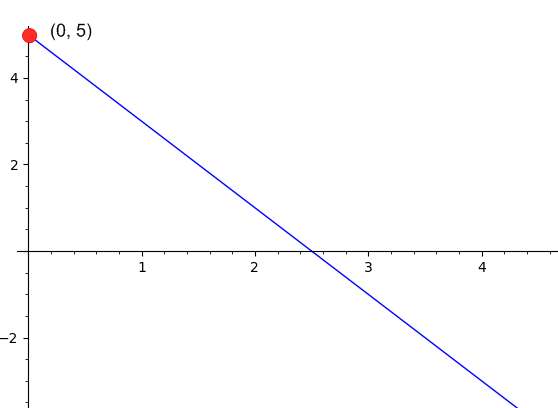
Example: Calculation of the Y-intercept given two lines

You know that a line passes through the points \(\left(\displaystyle \frac{1}{4}, 1\right)\) and \(\left(\displaystyle \frac{15}{2}, 6\right)\). Find the y-intercept of the line.

Solution: : Calculation of the y-intercept of the line

The information provided about the line is that the line passes through the points\(\displaystyle \left( \frac{1}{4}, 1\right)\) and \(\displaystyle \left( \frac{15}{2}, 6\right)\)

Therefore, the first step consists in computing the slope. The formula for the slope is: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Now, by plugging the corresponding numbers is , we get that the slope is: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 6 - 1}{ \displaystyle \frac{15}{2} - \frac{1}{4}} = \frac{ \displaystyle 6-1}{ \displaystyle \frac{15}{2}-\frac{1}{4}} = \frac{20}{29}\]

So then, now we know that the slope is \(\displaystyle m = \frac{20}{29}\) and that the line passes through the point \(\displaystyle \left( \frac{1}{4}, 1\right)\)

Hence, with the information we have, we can construct directly the point-slope form of the line, which is

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

and then plugging the known values of \(\displaystyle b = \frac{20}{29}\) and \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{4}, 1\right)\), we get that

\[\displaystyle y-1 = \frac{20}{29} \left(x-\frac{1}{4}\right)\]

Now, we need to expand the right hand side of the equation by distributing the slope, so we get \[\displaystyle y = \frac{20}{29} x + \frac{20}{29} \left(-\frac{1}{4}\right) + 1\]

and simplifying we get that \[\displaystyle y=\frac{20}{29}x+\frac{24}{29}\]

Conclusion : Based on the data provided, we conclude that the line crosses the y-axis at \(\displaystyle y = \frac{24}{29}\), hence, the corresponding y-intercept point is \(\displaystyle \left(0, \frac{24}{29}\right)\).

Another calculation you may be interested too is the one using our x-intercept calculator , which is the point where the line crosses the x-axis.

The intercepts of a line provide an excellent graphical intuition of what the line is doing, and they have direct applications when solving systems of equations , or in economics when computing consumer and producer surpluses.