Double Angle Formula
Instructions: Use this Double Angle Formula to compute the trigonometric values of the double angle, for a given angle \(\theta\), in the form below:
Double Angle Formula Calculator
This double angle formula calculator will allow you to provide a certain angle in radians, and get all the trig values of the corresponding double angle. In simple words, this a calculator to compute things like sin(2x) in terms of the trig values for x.
Notice that the angle needs to be expressed in radians. If you have it in degrees, you can use this degrees to radians calculator to make the conversion.
One interesting element about the trigonometric functions is that there is a way to compute the value of the trigonometric function of the double of a given angle, by using relatively simple formulas, by using the so-called double angle formulas.
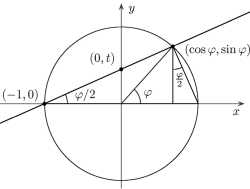
What is the formula for double angle?
Assume that we have an angle \(\theta\) that is measured in radians, and the \(2 \theta\) is the double angle. Then, the following double angle identities formulas are used for the double angle
\[\sin(2\theta) = 2\sin(\theta) \cos(\theta)\] \[\cos(2\theta) = \cos^2(\theta) - \sin^2(\theta)\] \[\tan(2\theta) = \displaystyle \frac{2\tan(\theta)}{1-\tan^2(\theta)}\]What is cool about these formulas is that if know the trigonometric values for an angle \(\theta\), you can use the formulas above for to compute the trigonometric formulas for \(2\theta\). So, say that you know the trigonometric values for 30 o , then you can use the formulas above to compute the trigonometric values for 60 o
These are the formulas that this double angle calculator will provide to you once a valid angle in radians is provided.
Example of using double angles
Double Angle formula Example: We know that \(\sin(45^o) = \sin(45^o) = \displaystyle \frac{\sqrt{2}}{2} \). Let us compute \(\sin(90^o)\). Notice that \(90^o\) so the double angle of \(45^o\), so then, using the above formula
\[\sin(90^o) = \sin(2\cdot 45^o) = 2\sin(45^o) \cos(45^o) =\displaystyle 2 \cdot\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2}}{2} = 2 \cdot \frac{2}{4} = 1\]What do you use the double angle for?
We said that the double angle could be very useful for calculation purposes, but actually, it is more of a theoretical use for them. I mean, trigonometric tables are not computed using the double angle starting from some notable angles, but using Taylor approximation instead.
Double angle formulas are extremely useful in identities used to make certain calculation of trigonometric integrals possible.
Tightly related, and conceptually equivalent, you can use these half angle formulas to compute the trigonometric value of the half angle \(\frac{\theta}{2}\) given the trigonometric values of \(\theta\).
Example of double angle calculation (including tangent double angle)
Question: Use a double angle formula for sine, cosine and tangent, for the original angle: \(\theta = \frac{\pi}{8}\).
Solution: This something you can easily do with this double angle identities calculator. We are given the angle \(\theta = \frac{\pi{}}{8}\) radians. The following double angle formulas are used to find the trigonometric values of the corresponding double angle \(2\theta\).
For Sine:
\[ \begin{array}{ccl} \sin(2\theta) & = & \displaystyle \sin(2 \cdot \frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle 2 \sin(\frac{\pi{}}{8}) \cos(\frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle 2 \times 0.383 \times 0.924 \\\\ \\\\ & = & 1 \end{array}\]Now for Cosine:
\[ \begin{array}{ccl} \cos(2\theta) & = & \displaystyle \cos(2 \cdot \frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle \cos^2(\frac{\pi{}}{8}) - \sin^2(\frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle 0.924^2 - 0.383^2 \\\\ \\\\ & = & \displaystyle 0.8538 - 0.1467 \\\\ \\\\ & = & 0.707 \end{array}\]Now for Tangent:
\[ \begin{array}{ccl} \tan(2\theta) & = & \displaystyle \cos(2 \times \frac{\pi{}}{8}) \\\\ \\\\ & = & \displaystyle \frac{2 \tan(\frac{\pi{}}{8})}{1-\tan^2(\frac{\pi{}}{8})} \\\\ \\\\ & = & \displaystyle \frac{2 \times 0.414}{1-0.1714} \\\\ \\\\ & = & 0.999 \end{array}\]Therefore, based on the angle provided \(\theta = \frac{\pi{}}{8}\) radians, the corresponding double angle expressions are \(\sin(2\theta) = 1\), \(\cos(2\theta) = 0.707\) and \(\tan(2\theta) = 0.999\).

