Inverse Function Calculator
Instructions: Use this calculator to find the inverse function for a function you provide, showing all the steps. Please type in the function expression you want to find the inverse for in box below.
More on this Inverse Function Calculator
This calculator will allow you to find the inverse of a given function showing all the steps, assuming that the inverse exists. The calculator will examine the function solve an equation associated to the definition of the function, and it will try to assess whether or not an inverse exist.
For example, you can provide a linear function like 'f(x) = 3x - 2', which would be a simple case, or for example you could take it up a notch with something a bit harder, like with a rational function like 'y = (x-1)/(x-3)'.
Once you provide a valid function, please click on "Calculate" button to get all the steps of the process shown to you, with the inverse function as the final answer, if an inverse exist, or with the explanation that no solution could be found and why.
It is not guaranteed that you will find all inverse functions. For one, not all functions have an inverse, and second (as we will see in the next section), the process of finding the inverse involves solving for x for an equation, and as we know, some equations can be very hard or impossible to solve.
So then, simpler functions are more likely to be amenable for finding their inverse, in case the inverse exists.

How do you define the inverse of a function?
In layman's terms, the inverse of a function is the function that does the opposite as what the original function does. So, think of a function in terms of y = f(x), and then you could think of it as you go from x to y. You feed the function with an x, and the function gives you an specific y.
The inverse function starts with the y, and finds the way back to x, in a way that the x is the same that led to y through the original function. Now, the formal definition is done via function composition . For a function \(f\), we say that \(g\) is the inverse function of \(f\) if
\[ f(g(x)) = x \]and
\[ g(f(x)) = x \]for all x in a certain set. There is more to it, but we will leave it at the intuitive level (Strictly speaking, a function needs to be injective and surjective in order to be invertible, and some other technicalities that are considering, like restricting the domain and range , etc.)
Usually, we call \(f^{-1}\) to the inverse of \(f\), so the formula that defines the inverse is typically written as:
\[ f(f^{-1}(x)) = x \]What are the steps to find the inverse function
- Step 1: Start with the equation that defines the function, this is, you start with y = f(x)
- Step 2: You then use algebraic manipulation to solve for x. Depending on how complex f(x) is you may find easier or harder to solve for x.
- Step 3: In some circumstances you will simply not be able to solve for x, for complex non-linear functions f(x)
- Step 4: If you are able to solve for x, then you should be able to write x = g(y)
- Step 5: You need to assess whether the solution found is unique. This is, could solve for x uniquely. In other words, did you find only one solution when solving for x? If yes, then you have an inverse function, otherwise, there is no inverse
- Step 6: If you found the inverse by solving x = g(y), you simply change the name of the variable and write f -1 (x) = g(x), which makes the emphasis in that g(x) IS the actual inverse
If you were to use Calculus and derivatives (but notice that you DON'T need derivatives to compute the inverse), you could find the derivative of the function, and make sure that the derivative is always positive or negative, to ensure the function is injective, and hence, invertible.
But usually, the methodology of solving for x is a lot more palatable for basic Algebra students.
The rule for finding inverse functions
The are actually no other rules to compute the inverse function other than starting with y = f(x) and then solving for x. A rule like that sounds pretty broad, because it is. More than a rule, it is a generic methodology for getting started in the process.
Ultimately calculating the inverse will depend on your success of solving an equation, and making sure that solution is unique. It does help to assess the graph of the function beforehand, so to not to look for an inverse when there is clearly none.
What to look in a graph? A function needs to be monotone (increasing or decreasing) on a certain subdomain in order to be invertible. With that being said, we could conveniently restrict the domain of a function to a smaller subdomain to find the inverse in a smaller set, that is always a possibility.

How do we know for sure that the function has an inverse?
Formally, the only way of making sure a function has an inverse, you need to ensure the function is injective (1-to-1). This is assessed either by computing its derivative (if it exists) and making sure it is either positive and negative everywhere, or by manually ensuring that when we start with y = f(x) and we solve for x, we always get a unique solution.
This can be also seen graphically, using the horizontal line test: You draw an arbitrary horizontal line, and the function f(x) passes the horizontal line test if any horizontal line drawn crosses the graph of the function at most once.

Example: Finding the inverse function
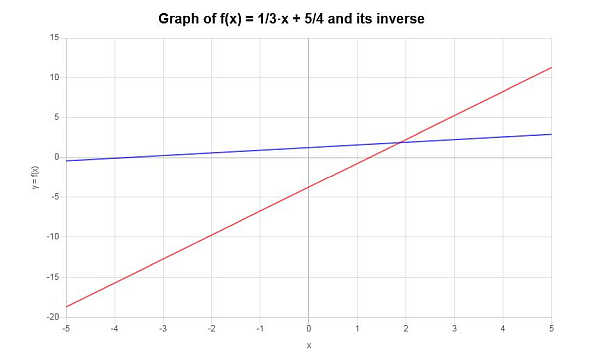
Find the inverse of the following function: \(f(x) = \displaystyle \frac{1}{3} x + \frac{5}{4}\)
Solution:
We have the following function:
\[f(x) = \frac{1}{3} x + \frac{5}{4}\]Then, in order to find the inverse of the given function, we need to solve for \(x\) and determine whether there is a solution or not. The starting equation is:
\[y = \displaystyle \frac{1}{3}x+\frac{5}{4}\]Step 0: In this case, we first need to simplify the given linear equation, and in order to do so, we conduct the following simplification steps:
Solving the Linear Equation
Putting \(x\) on the left hand side and \(y\) and the constant on the right hand side we get
\[\displaystyle -\frac{1}{3}x = -y -\left(-\frac{5}{4}\right)\]Now, solving for \(x\), by dividing both sides of the equation by \(-\frac{1}{3}\), the following is obtained
\[\displaystyle x=-\frac{1}{-\frac{1}{3}}y+\frac{\frac{5}{4}}{-\frac{1}{3}}\]and simplifying we finally get the following
\[\displaystyle x=3y-\frac{15}{4}\]Therefore, the solving for \(y\) for given linear equation leads to \(x=3y-\frac{15}{4}\).
Therefore, and since when solving for \(x\) we find a solution and it is only one solution, we have found the inverse.
The Inverse Function
Based on the work shown above, it can be concluded that the inverse function is:
\[f^{-1}(x) = 3x-\frac{15}{4}\]The inverse function can be depicted graphically as follows:
Example: More inverse examples
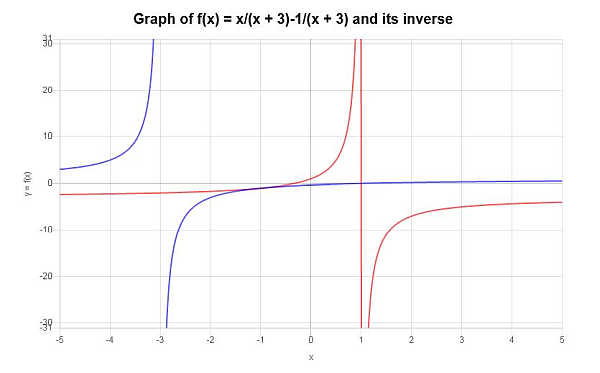
Compute the inverse function of: \(y = \frac{x-1}{x+3}\)
Solution:
In order to find the inverse of the given function, we solve for \(x\) and determine whether there is a solution or not. The starting equation is:
\[y=\frac{x-1}{x+3}\]The following is obtained:
Auxiliary Numerator Equation
We need to set the numerator equal to zero and find the solutions. Then, those roots that do not make the denominator equal to zero will be solutions to the rational equation
Using algebraic manipulation the above polynomial equation, the following is obtained:
\[x = -\frac{3y+1}{y-1} \]Auxiliary Denominator Equation
We find the roots of the denominator: \(x+3=0\)
Therefore, the solving for \(x\) for given linear equation leads to \(x=-3\).
Putting Together the Solutions of the Rational Equation
Then, by checking that we don't have a zero of the denominator, we find the following solution set to the equation \(\displaystyle y=\frac{x-1}{x+3}\) is
\[x = -\frac{3y+1}{y-1} \]Since when we solve for \(x\) we find one and only one solution, we conclude that we have an inverse function.
Finding the Inverse Function
Based on the work shown above, it can be concluded that the inverse function is:
\[f^{-1}(x) = -\frac{3x+1}{x-1}\]The inverse function found can be depicted graphically as follows:
Example: Not all functions have inverse
Does the following function have an inverse: \( y = \displaystyle \frac{1}{3} x^2 - \frac{2}{5} \) ?
Solution: Observe that
\[ y =\displaystyle \frac{1}{3} x^2 - \frac{2}{5} \] \[ \displaystyle \Rightarrow y + \frac{2}{5} = \frac{1}{3} x^2 \] \[ \displaystyle\Rightarrow x^2 = 3\left(y + \frac{2}{5} \right) \] \[\displaystyle \Rightarrow x = \pm \sqrt{ 3\left(y + \frac{2}{5} \right) }\]which indicates that there are two solutions, and then, there is no inverse in this case.
More function calculators
Functions are a crucial object in Math, especially in Calculus and Algebra, where lots of associations between variables are established via functions.
There are lots of things you can do with function: you can simplify them , you can differentiate a function , you can operate them, find the composite with another function, and the list goes on an on.
Many times, even if you are mentioning functions explicitly, you have functions underlying the whole process. So they are there, even if sometimes you don't know it. One great thing is that even with very complicated ones, you can always graph a function to get an idea of its behavior, so to at least make an educated of what the function does (goes up, goes down, etc).