More about this vertex calculator

This calculator will allow you to get a quadratic function that you provide into vertex form, showing all the steps. You need to provide a valid quadratic expression in x. Any valid quadratic function will work.

For example, you can provide something like x^2 + 3x + 4, or perhaps you could provide an expression that is not simplified, like x^2 + 3x - 1/2 x + 3x^2 - 3.

Once you provide a valid quadratic function, you just click on "Calculate" and the calculation of the vertex form will be shown to you, with all the steps provided by this parabola calculator.

Every quadratic function that is validly defined will have a vertex form, from which it will be direct to get the coordinates of the vertex, and whether the parabola opens "upward" or "downward".

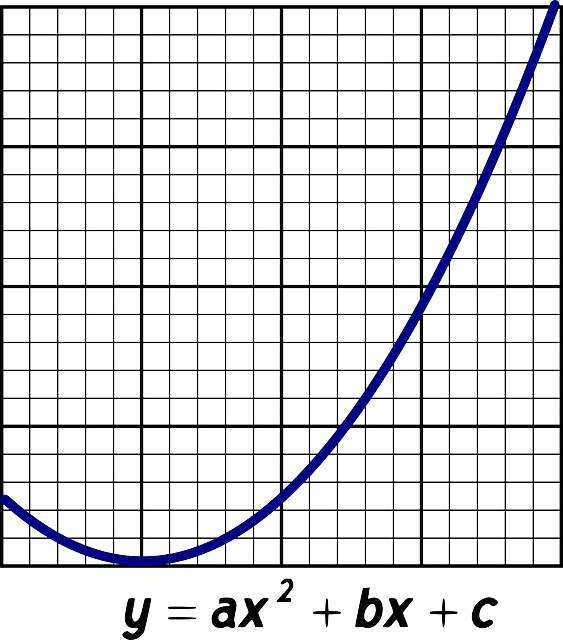
How to find the vertex form for a parabola?

All quadratic functions are graphically represented graphically by a parabola. This parabola will open upwards or downward, depending on the sign of the leading coefficient.

Ultimately, getting the parabola in vertex form consists of finding the vertex of the quadratic function, which is achieved by completing the square.

What are the steps calculating the vertex form?

So, how do you find the vertex form? You can follow these steps:

• Step 1: Identify the quadratic function. The expression has to have degree 2, and the leading coefficient multiplying x² needs to be different from zero
• Step 2: If the leading coefficient that multiplies x² is positive, the parabola opens upwards, and if it is negative, it opens downwards
• Step 3: Complete the squares, and notice the term inside the parentheses with x, because it determines the x-coordinate of the vertex
• Step 4: After completing the squares, the constant outside of the parenthesis (it could be zero) corresponds to the y-coordinate of the vertex

Therefore, we can see that the general process of vertex form calculation is tightly related with the process of completing the squares.

Is there a vertex formula?

As a matter of fact, yes, there is. Normally, the completion of squares process is the long way to go about it. Assume you have a quadratic function, expressed by:

\[ f(x) = a x^2 + b x + c\]

So, you already have a simplified quadratic function. The x-coordinate of the vertex is calculated using the following formula:

\[ x_v = \displaystyle \frac{-b}{2a} \]

Really simple, right? Yes. But then, how do you get the y-coordinate of the vertex? You take the value \(x_v\), and plug it into the quadratic function. So we get

\[ y_v = f(x_v) = a x_v^2 + b x_v + c \]

Naturally, this formula can be much faster than doing a process of completing the squares, but each method has its uses, and the circumstances of a given problem will tell you will form to use. .

Quadratic to Vertex form?

Why would you want to go from quadratic to vertex form? There are many reasons: from a geometric point of view, the vertex form allows use to see the given quadratic function as a translation and rescaling of an elementary parabola, where there translation is determined by the vertex, and the scale is determine with the leading coefficient.

The calculation may be labor intensive, but this parabola calculator will do the grunt work for you.

Standard to Vertex form?

There is usually a bit of confusion about this. Let me clarify, the vertex form is another name given to the standard form. So then then, the standard form of a quadratic function \(y = a(x-h)^2 + k\) is the same as the vertex form.

The confusion stems out because sometimes people use the general form of a quadratic when they refer to the standard form. The general form is \(y = ax^2 + bx + c\).

So, the question that makes sense is how to go from general form to vertex form, which is the same as asking how to go from the general form to the standard form. The answer is simple: Start from the general form and then you complete the squares to get to the standard form.

Example: How to find vertex form

Find the vertex of the following quadratic expression \(f(x) = x^2 + 3x - 6\) using the vertex formula

Solution: We need to find the vertex form for the the quadratic function \(\displaystyle f(x)=x^2+3x-6\).

We first compute the coordinates of vertex for the parabola associated to the given quadratic function.

For a quadratic function of the form \(f(x) = a x^2 + bx + c\), the x-coordinate of the vertex is computed using the following formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In this case, we have that the function for which we need to find the vertex for is \(f(x) = \displaystyle x^2+3x-6\), which implies that corresponding coefficients are:

\[a = 1\] \[b = 3\] \[c = -6\]

Plugging the known values of \(a\) and \(b\) into the formula for the x-coordinate of the vertex, we get:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{3}{2 \cdot 1} = -\frac{3}{2}\]

Now, we need to plug the value of \(x_V = \displaystyle -\frac{3}{2}\) into the quadratic function, so we get:

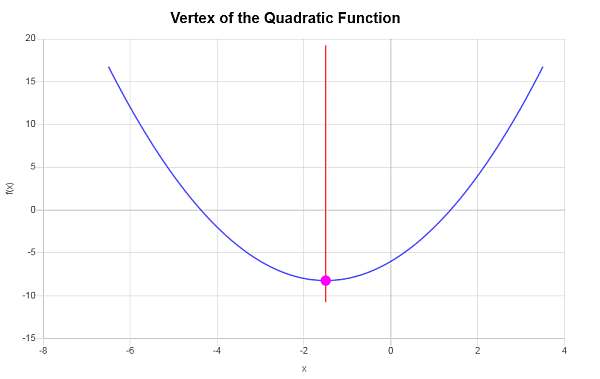
\[y_V = f(x_V)\] \[ = 1\cdot \left(-\frac{3}{2}\right)^2+3\cdot \left(-\frac{3}{2}\right)-6=1\cdot\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}+3\cdot \left(-\frac{3}{2}\right)-6=\frac{9}{4}-\frac{9}{2}-6=-\frac{33}{4}\]

Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -\frac{3}{2}\), and the y-coordinate of the vertex is \(y_V = \displaystyle -\frac{33}{4}\). This indicates that the point that represents the vertex is \( \displaystyle \left(-\frac{3}{2}, -\frac{33}{4}\right)\).

The following is obtained graphically:

We need to complete the square for the quadratic expression \(\displaystyle x^2+6x-2\).

The following steps need to be taken in order to complete the square:

Step 1: In this case since the leading constant, the term that multiplies \(x^2\) in the given polynomial, is \(a = 1\), so then we don't to factor it out.

Step 2: We force a '2' in front of the term \(x\) by observing that term of order 1 in the given quadratic expression can we rewritten: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), so then we get \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Step 3: The term that multiplies 2 in this case is \(\displaystyle 3\), so in order to use the binomial equation, we need its square \(\displaystyle \left(3\right)^2\) to be in the expression.

In order to achieve that, we now add and subtract the term \(\displaystyle \left(3\right)^2 = 9\), so to complete the square. Adding and subtracting the same term is the same as adding zero, so it does not affect the expression: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Step 4: We complete the square and simplify the constants: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusion: Therefore, we find that the function in vertex form is \(\displaystyle f(x) = \left( x+3 \right)^2-11\), which completes the calculation.

Example: Quadratic to vertex form

Convert the following quadratic form \(f(x) = x^2 + 6x - 2\) into vertex form. What are the coordinates of the vertex? Does the parabola opens upward or downward?

Solution:

We need to find the vertex form for the the quadratic function \(\displaystyle f(x)=x^2+6x-2\).

We first compute the coordinates of vertex for the parabola associated to the given quadratic function.

For a quadratic function of the form \(f(x) = a x^2 + bx + c\), the x-coordinate of the vertex is computed using the following formula:

\[x_V = \displaystyle -\frac{b}{2a}\]

In this case, we have that the function for which we need to find the vertex for is \(f(x) = \displaystyle x^2+6x-2\), which implies that corresponding coefficients are:

\[a = 1\] \[b = 6\] \[c = -2\]

Plugging the known values of \(a\) and \(b\) into the formula for the x-coordinate of the vertex, we get:

\[x_V = \displaystyle -\frac{b}{2a} = \displaystyle -\frac{6}{2 \cdot 1} = -3\]

Now, we need to plug the value of \(x_V = \displaystyle -3\) into the quadratic function, so we get:

\[y_V = f(x_V)\] \[ = 1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=1\cdot \left(-3\right)^2+6\cdot \left(-3\right)-2=-3^2+6\cdot \left(-3\right)-2=9-18-2=-11\]

Therefore, the x-coordinate of the vertex is \(x_V = \displaystyle -3\), and the y-coordinate of the vertex is \(y_V = \displaystyle -11\). This indicates that the point that represents the vertex is \( \displaystyle \left(-3, -11\right)\).

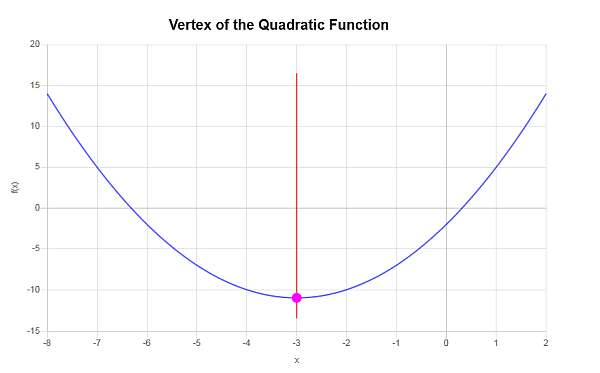
We need to complete the square for the quadratic expression \(\displaystyle x^2+6x-2\).

The following steps need to be taken in order to complete the square:

Step 1: In this case since the leading constant, the term that multiplies \(x^2\) in the given polynomial, is \(a = 1\), so then we don't to factor it out.

Step 2: We force a '2' in front of the term \(x\) by observing that term of order 1 in the given quadratic expression can we rewritten: \(\displaystyle 6 x = 2 \cdot \left(3\right) x\), so then we get \[ x^2+6x-2 = x^2+2 \cdot \left(3\right) x-2 \]

Step 3: The term that multiplies 2 in this case is \(\displaystyle 3\), so in order to use the binomial equation, we need its square \(\displaystyle \left(3\right)^2\) to be in the expression.

In order to achieve that, we now add and subtract the term \(\displaystyle \left(3\right)^2 = 9\), so to complete the square. Adding and subtracting the same term is the same as adding zero, so it does not affect the expression: \[ \begin{array}{ccl} \displaystyle x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \end{array}\]

Step 4: We complete the square and simplify the constants: \[ \begin{array}{ccl} x^2+6x-2 & = & \displaystyle x^2+2 \cdot \left(3\right) x-2 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x-2+9-9 \\\\ \\\\ & = & \displaystyle x^2+2 \cdot \left(3\right) x+9-2-9 \\\\ \\\\ & = & \displaystyle \left[x^2+2 \cdot \left(3\right) x+\left(3\right)^2\right]-2-9 \\\\ \\\\ & = & \displaystyle \left( x+3 \right)^2-11 \end{array}\]

Conclusion: Therefore, we find that the function in vertex form is \(\displaystyle f(x) = \left( x+3 \right)^2-11\), which completes the calculation.

Other quadratic calculators

Most of quadratic calculators rely in one way or the other on the process of completing the squares, which allows to group things inside of parentheses that are squared.

As we can see in the vertex formula, the vertex calculation is tightly linked with the quadratic formula and the calculation roots of the quadratic equation. .