More about Trig Derivatives

Use this calculator to find trigonometric derivatives, which in this case we assume to be any valid differentiable function that involves one or more elementary trig function.

One example of a valid function for this calculator is f(x) = sin(x)/x, or f(x) = x*sin(x^3), just to given an example.

Then, when you have already typed the corresponding function, you can then click on the "Calculate" button, so to get all the steps of the calculation of the derivative shown to you.

Trigonometric functions play a crucial role in calculus, as well in calculating derivatives in general. Ultimately, more complex functions can get their derivatives reduced to the calculation of the derivative for simpler trig functions.

Basic Trig Derivatives

The idea of using derivative rules is to break down a complex function and differentiate it by using the derivatives of known functions. Specifically, simple trig functions like sine, cosine, tangent and cotangent will play an important role in that.

What are the basic trig derivatives?

• Trig Derivative 1: \(\frac{d}{dx} \sin (x) = \cos(x)\)
• Trig Derivative 2: \(\frac{d}{dx} \cos (x) = -\sin(x)\)
• Trig Derivative 3: \(\frac{d}{dx} \tan (x) = \sec^2(x)\)
• Trig Derivative 4: \(\frac{d}{dx} \cot (x) = -\csc^2(x)\)
• Trig Derivative 5: \(\frac{d}{dx} \sec (x) = \sec(x)\tan(x)\)
• Trig Derivative 6: \(\frac{d}{dx} \sec (x) = -\csc(x)\cot(x)\)

These are the basic derivatives that you need to know very, and possibly memorize in order to use derivative rules to compute more complicated derivatives

Are trig derivatives in degrees?

No, the derivative of trig functions are in radians, so the trig derivatives found reflect the fact that the argument x is measured in radians.

So, for example, assume that we wanted to compute the derivative of sin in degrees, so we define \(f(y) = \sin(y)\), where \(y\) is measured in degrees.

Now, let \(x = \frac{\pi y}{180}\) be the equivalent angle in radians and also solving for \(y\) we find that \(y = \frac{180 x}{\pi}\), so then using the Chain Rule:

\[\displaystyle \frac{d}{dy} f(y) = \displaystyle \frac{d}{dy} f(y(x)) \frac{dy}{dx} = \frac{180}{\pi} \cos(y) \]

So based on this, the derivative of sine in degrees is actually cosine in degrees, but times a factor \(\frac{180}{\pi}\).

How do you find derivatives in trigonometry?

Trig derivatives are found by definition, using basic trig identities. For example, using the sine of the sum formula we can derive the derivative of \(\sin(x)\), using the definition of limit:

\[\displaystyle \frac{d}{dx} \sin(x) = \displaystyle \lim_{h \to 0} \frac{\sin(x+h)-\sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)\cos(h) + \cos(x)\sin(h) - \sin(x)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0} \frac{\sin(x)(\cos(h)-1) + \cos(x)\sin(h)}{h} \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} + \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \displaystyle \lim_{h \to 0}\left( \frac{\sin(x)(\cos(h)-1)}{h} \right)+ \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \displaystyle \lim_{h \to 0} \left( \frac{(\cos(h)-1)}{h} \right)+ \cos(x) \displaystyle \lim_{h \to 0}\left( \frac{\cos(x)\sin(h)}{h} \right) \] \[\displaystyle = \sin(x) \cdot 0 + \cos(x) \cdot 1 = \cos(x)\]

Tips and Tricks

The main takeaways for you is to always remind what the 6 trig derivatives are, and know them by heart, as you will used them continuously, along with the basic differentiating rules.

Similarly, you can use trig identities and the definition of inverse function to find the most common inverse trig derivatives.

Example: Trig Derivative calculation

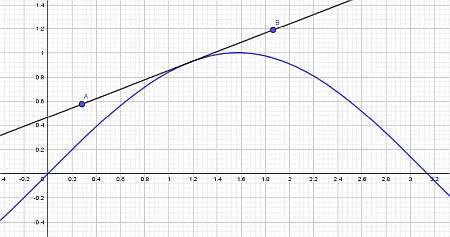
Consider the following function: \(f(x) = \sin^2(x)+ \frac{1}{x}\). Find its derivative

Solution: Trig derivatives involve trig function that need to be differentiated. Consider the function \(\displaystyle f(x)=\sin\left(x\right)^2+\frac{1}{x}\), which contains a sine function, so it qualifies as a trig derivative.

Results: For this example, it is found that the derivative is:

\[f'(x) = \frac{2x^2\cos\left(x\right)\sin\left(x\right)-1}{x^2}\]

It is very useful to depict the function and its derivative on a graph. See below:

Example the derivative of a trig function

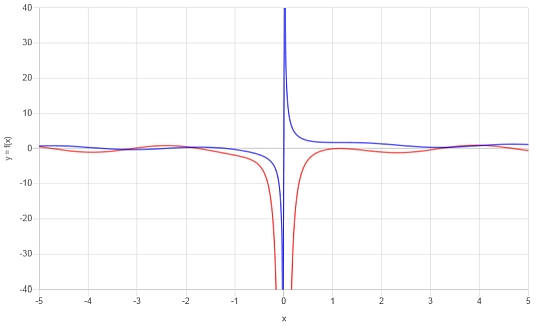
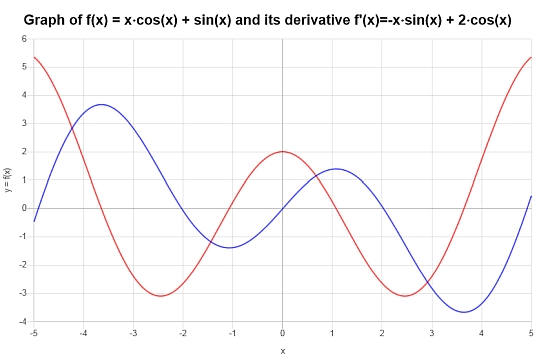
Consider the following trig function: \(f(x) = \sin(x) + x \cos(x)\), find its derivative.

Solution: Now, we need to work with the derivative of the following trig function \(\displaystyle f(x)=\sin\left(x\right)+x\cos\left(x\right)\).

Final Conclusion: We conclude that the derivative is given by:

\[f'(x) = -x\sin\left(x\right)+2\cos\left(x\right)\]

The following plot is obtained:

Example: Trig derivatives and implicit differentiation

Find \(\frac{dy}{dx}\) for \( \sin(x)+\cos(y) = 1 \).

Solution: We need to use implicit differentiation, so we differentiate both sides and use the chain rule:

\[ \frac{dy}{dx}\left(\sin(x)+\cos(y)\right) = \frac{dy}{dx} \left(1\right) \] \[\Rightarrow \cos(x)-\sin(y)y' = 0 \] \[\Rightarrow \sin(y)y' = \cos(x) \] \[\Rightarrow y' = \frac{\cos(x)}{\sin(y)} \]

which concludes the calculation.

Other useful derivative calculators

Finding the derivative of simple and elementary functions is the cornerstone of the process of finding the derivatives of more complicated functions, via the use of the well known differentiation rules.

In this context, basic trigonometric functions can be considered elementary functions for which the derivative can be calculated using limits, via its very definition. Among the most useful elementary functions we have polynomials and rational functions.