More about this System of Equations to Matrix Form Calculator

One crucial ability when solving systems of linear equations is to be able to pass from the traditional format of linear systems to matrices.

One you have the matrix representation of a linear system, then you can either apply Cramer's Rule or you can solve the system by first finding the inverse of the corresponding matrix of coefficients.

Or, with the matrix representation you can build the augmented matrix and conduct Gauss pivoting method, whichever suits you best.

First: How do you write a system of equations in matrix form?

Step 1: Identify each of the equations in the system. Each equation will correspond to a row in the matrix representation.

Step 2: Go working on each equation. For each of them, identify the left hand side and right hand side of the equation.

Step 3: What is on the left hand side will be part of the matrix A, and what is on the right hand side will be part of the vector b

Step 4: The coefficients on the left need to be identified separately in term of which coefficient multiplies each variable.

Step 5: Each equation represents a row, and each variable represents a column of the matrix A.

How do you use a matrix to solve a system of equations?

Once you have a system in matrix form, there is variety of ways you can proceed to solve the system. Usually, you start first with computing the determinant of the matrix, as an initial criterion to know about the solutions of the system.

When \(\det A \ne 0\), then we know the system has a unique solution. Now, when \(\det A = 0\), it does not mean you don't have solutions, it only means that if there are solutions, it is not unique.

Indeed, when \(\det A = 0\), you cannot use Cramer's Method or the inverse method to solve the system of equations. In that case, you are better off using Gauss pivoting method.

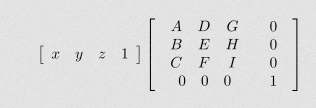
How to solve matrix equations

Often times, you are given a system of equations directly in matrix format. If that is the case, and the number of equations is the same as the number of variables, you can try to use the inverse method or Cramer's Rule. Otherwise, you can use Gauss method.

Now, you can use this calculator to express a system in a traditional form when given a matrix form.