About this Tangent Line Calculator

This calculator will allow you to seamlessly conduct the calculations required to get the tangent line of a function, at a given point, showing all the steps.

All you need to do is to provide a valid function f(x), and a point where you want the tangent line at. The function could be any valid, differentiable function like f(x) = sin(x), or f(x) = x^2 - x + 1, etc. The point can be any valid numeric expression, like 1/2 for example.

Then, when the required information has been provided, and it is valid, you need to click on "Calculate" to get all the steps of the tangent line equation shown to you.

Tangent line applications abound in science all around. Also called first order or linear approximation, it has some really deep meaning in Physics and Engineering, where the idea of the main contribution to change (the first order part) is one that unveil a lot of information about a process.

What is the tangent line

In simple terms, a tangent line is a line that intersects a curve, but it intersects it at one point only (at least locally). This tangent line is constructed by fixing a point \(x_0\) and then taking a different point \(x_1\).

Then, by constructing the line that passes through the points \((x_0, f(x_0))\) and \((x_1, f(x_1))\), we get what is called a secant line, as shown in the graph below:

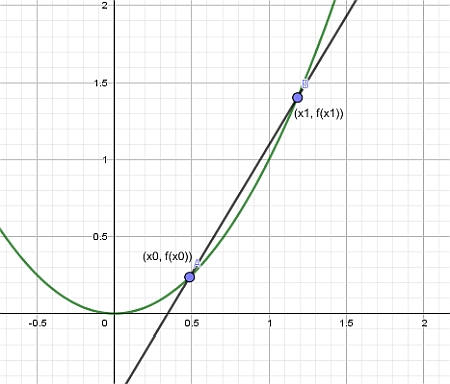
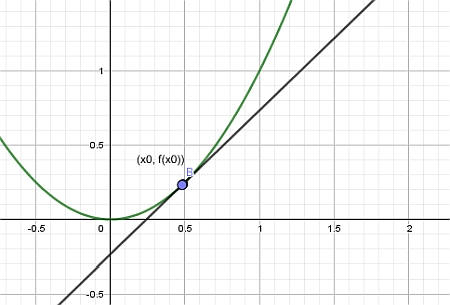
Finally, we let the point \(x_1\) approach to \(x_0\), and what we get is the tangent line:

Steps for finding the tangent line geometrically

• Step 1: Identify the function f(x) you want to work with, and the point x0. You need both of them
• Step 2: The point (x0, f(x0)) will be on the curve of the function f(x). Plot it
• Step 3: Choose a point (x1, f(x1)), for an x1 that is different from x0 (can be to the left or right of x). Plot it
• Step 4: Draw a line passing through the points (x0, f(x0)) and (x1, f(x1))
• Step 5: Choose a point x2 that is halfway between x0 and x1, and draw a line passing through the points (x0, f(x0)) and (x2, f(x2))
• Step 6: Repeat this process a few times

This graphical method will aid you at getting a rough idea of how the tangent line looks like, but is an approximation (unless the function f(x) is linear).

Tangent Line Formula

The approximation method using secant lines can give you an idea of what you are looking for, but fortunately, there is an exact formula to compute the tangent line to a function at a point \(x_0\). The tangent line formula is:

\[\displaystyle y = f(x_0) + f'(x_0) (x - x_0) \]

Simple, huh? In simple terms, this formula is telling that that the tangent line is a line that passes through the point \((x_0, f(x_0))\) and that has a slope of \(m = f'(x_0)\)

Then, in easy terms, the slope of the tangent line at a given point is exactly the derivative of the function at that point.

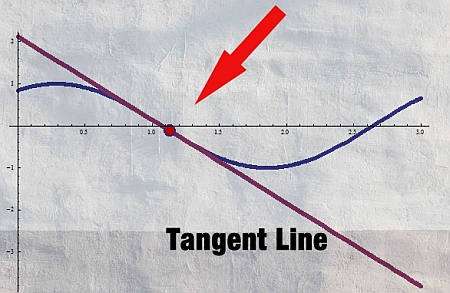
Steps for applying the tangent line formula

• Step 1: Identify the function f(x) and the point x0
• Step 2: Compute the value of the function at x0, which is f(x0)
• Step 3: Compute the derivative of f(x) at point x0, so you need f'(x0)
• Step 4: Directly apply the formula of the tangent line \(y = f(x_0) + f'(x_0) (x - x_0)\)

Once you have the equation of the line, you can transform it into the format that it is most useful to the situation at hand.

The slope of the tangent line

One of the key takeaways is that the slope of the tangent line at \(x_0\) is exactly \(f'(x_0)\), which is the derivative at the point \(x_0\). This provides a clear and extremely useful interpretation of the derivative in geometric terms.

This connection allows to find the equation of the tangent line to a given curve at a given point by simply looking at the derivative of the function.

When do you have a horizontal tangent line?

A horizonal tangent line will occur when the point chosen \(x_0\) when the corresponding derivative at that point is equal to zero. In that case the tangent line (which is the line that touches the curve at one point locally) will be parallel to the y-axis.

So, all you need to know in order to identify horizontal tangent lines is to find points where the derivative of the function is zero.

When do you have a vertical tangent line?

A vertical tangent line will occur when the derivative is "infinite" at a point. This is a simple way to say that it is where the derivative is not defined at a given point, but it converges to infinite as we approach to the point.

For example, one could say that \(f(x) = \frac{1}{x}\) has a vertical tangent line at x = 0. Though, it could be argued that there is no tangent line because the derivative is not well defined at x = 0.

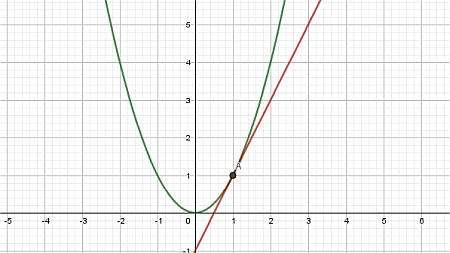
Example: Tangent Line

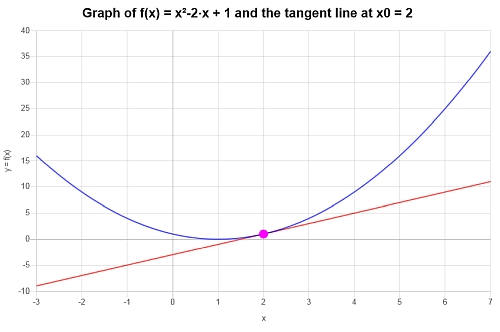
Find the equation of the tangent line for \(f(x) = x^2 - 2x + 1\), at the point \(x_0 = 2\).

Solution: The following function is the one we need to work with: \(\displaystyle f(x)=x^2-2x+1\). First, we need to compute its derivative.

The function came already simplified, so we can proceed directly to compute its derivative:

Tangent Line: The equation of the tangent line for the function \(\displaystyle f(x)=x^2-2x+1\) at the point \(x_0 = 2\) is:

\[y = y_0 + f'(x_0)(x - x_0) \]

In this case, \(\displaystyle y_0 = f(x_0)\), so then plugging the value of the point \(x_0 = 2\) in the function leads to:

\[y_0 = f(x_0) = f(2) = 2^2-2\cdot 2+1 = 1 \]

Also, plugging the value of the point \(x_0 = 2\) at the calculated derivative leads to:

\[f'(x_0) = f'(2) = 2\cdot 2-2 = 2 \]

So then, we now plug in these values into the tangent line formula to get:

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = 1+2\left(x-2\right) = 2x-3 \]

Conclusion: Therefore, it is found that the tangent line for the function \(\displaystyle f(x)=x^2-2x+1\) at the point \(x_0 = 2\) is:

\[y = 2x-3 \]

The following plot is obtained for the given function and its tangent line at \(x_0 = 2\):

Example: Tangent line equation

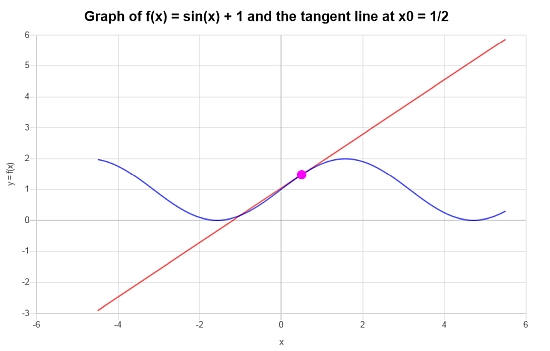
What is the tangent line at x = 1/2, for the function \(f(x) = \sin(x) + 1\)?

Solution:

The following function has been provided: \(\displaystyle f(x)=\sin\left(x\right)+1\), for which we need to compute its derivative.

The function came already simplified, so we can proceed directly to compute its derivative:

Tangent Line: We find that the corresponding equation of the tangent line at the point \(x_0 = \frac{1}{2}\) is given by:

\[y = y_0 + f'(x_0)(x - x_0) \]

But in this specific case, \(\displaystyle y_0 = f(x_0)\), which means that we need to plug in the value of the point \(x_0 = \frac{1}{2}\) at the function, so we get:

\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \sin\left(\frac{1}{2}\right)+1\]

Now, doing the same at the derivative, for \(x_0 = \frac{1}{2}\) we find

\[f'(x_0) = f'\left(\frac{1}{2}\right) = \cos\left(\frac{1}{2}\right) \]

Now we just need to plug the values in, so we find that

\[y = y_0 + f'(x_0)(x - x_0) \]\[\Rightarrow y = \sin\left(\frac{1}{2}\right)+1+\cos\left(\frac{1}{2}\right)\left(x-\frac{1}{2}\right) = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Conclusion: We find that the corresponding tangent line we are looking for, at the corresponding point \(x_0 = \frac{1}{2}\) is given by

\[y = x\cos\left(\frac{1}{2}\right)-\frac{1}{2}\cos\left(\frac{1}{2}\right)+\sin\left(\frac{1}{2}\right)+1 \]

Graphically:

Example: Another tangent line

What is the tangent line at x = 0, for the function \(f(x) = \cos(x)\)? Does this result make sense?

Solution: Observe that \(f'(x) = -\sin(x)\), so then \(f'(0) = -\sin(0) = 0\). This is, the tangent line has a slope of m = 0 at x = 0, so then the equation of the tangent line is simply \(y = y_0 = \cos(0) = 1\). This makes sense because in this case, the tangent line is a horizontal line.

More differentiation calculators

Some people may claim that differentiation is a relatively straightforward exercise, and that using a derivative calculator may be not needed, but in truth, the calculation of derivatives can still be fairly cumbersome and may require lengthy algebraic calculations.

When you have an expression with more than one variable, in order to find the derivative you will need to determine whether the variables are independent from each other, in which case you use partial derivatives, or if there is an equation that link the variables in which case you would need to use implicit differentiation.

The main two areas in differential calculus are integration and differentiation, and they both have their broad applications, everywhere. Partial derivatives appear in great length in Engineering and Economics applications.

On the one hand, differentiation deals with infinitesimal rates of change, whereas integration deals with summing up infinitesimal rates of change, and admirably so, they are tightly linked by the Fundamental Theorem of Calculus.