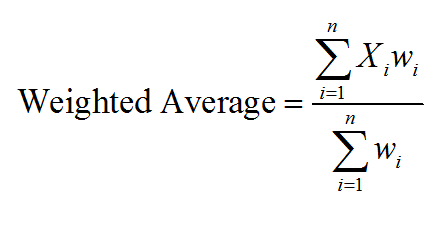What you need to know about this Weighted Average Calculator

The average, as a measure of central tendency is typically used in applications as a representative value, from a whole set of values \(X_1, X_2, ...., X_n\).

But sometimes, it turns out that not all values are equally important, and we would like to consider some values to be more important than others. This is achieved by using weights and the concept of weighted averages.

When to use weighted average?

As it was mentioned above, the weighted average needs to be used when not all values in the sample are equally important, or said differently, not all the values in the sample carry the same weight.

Then, in that case, for each value \(X_i\) we associate a weight \(w_i\), which is a positive number, and it represents how important \(X_i\). The larger the \(w_i\) is, the more important \(X_i\) is in terms of its representativeness.

Weighted average equation

The weighted average formula is based upon the values \(X_i\) and weights \(w_i\), and it corresponds to:

\[\text{Weighted Average}=\frac{\sum\limits_{i=1}^{n}{{{X}_{i}}{{w}_{i}}}}{\sum\limits_{i=1}^{n}{{{w}_{i}}}}\]

This weighted mean calculator will show you how to use the above formula step-by-step.

What if there are no weights?

Observe that if all the values in the data carry the same weight, this is, no value is more important than any other, then we should use this sample mean calculator , which does not go into the considering any weights to compute the average.

Is this the same as the Weighted average Excel

Well, the results should be the same, but for Excel you would typically use the approach of formulas. This is, you would compute a SUMPRODUCT first of values and weights, and then divide by the SUM of weights.

The difference of this calculator to what you would get in Excel, is that with this calculator you show the steps.

Application: Grade calculator

Use this weighted average calculator to calculate the grade in the following situation:

A student finish an Algebra course and got 88 points on HW's, 95 points on quizzes, 87 points on the midterm and 86 points on the final exam.

In the syllabus, the teacher wrote that HW's count 10%, quizzes 20%, the midterm 30%, and the final exam 40% of the final score. What is the student's grade?

Solution:

We need to compute the weighted average for the following provided data:

Values (\(X_i\))	Weights (\(w_i\))
88	0.10
95	0.20
87	0.30
86	0.40

What we need to do is to multiply each value by its weight, and the add them all up, and this result needs to be divided by the sum of weights. Mathematically:

\[\text{Weighted Average}=\frac{\sum\limits_{i=1}^{n} X_i w_i}{\sum\limits_{i=1}^{n} w_i}\]

The following table will aid us with the required calculations:

Values (\(X_i\))	Values (\(X_i\))	Weights (\(w_i\))	\(X_i \cdot w_i\)
88	88	0.10	\(88 \cdot 0.10 = 8.8\)
95	95	0.20	\(95 \cdot 0.20 = 19\)
87	87	0.30	\(87 \cdot 0.30 = 26.1\)
86	86	0.40	\(86 \cdot 0.40 = 34.4\)
Sum =	Sum =	\(1\)	\(88.3\)

\[ \begin{array}{ccl} \text{Weighted Average} & = & \displaystyle \frac{\sum\limits_{i=1}^{n} X_i w_i}{\sum\limits_{i=1}^{n} w_i} \\\\ \\\\ & = & \displaystyle \frac{1}{1} \left( {88 \cdot 0.10} + {95 \cdot 0.20} + {87 \cdot 0.30} + {86 \cdot 0.40} \right) \\\\ \\\\ & = & \displaystyle \frac{88.3}{1} \\\\ \\\\ & = & 88.3 \end{array}\]

Therefore, based on the data provided, the weighted average in this case is \(88.3 \).