Polynomial Functions

This polynomial functions calculator will help you calculate polynomials functions, by calculating and simplifying any polynomial expression you provide.

You can provide any type of expression involving polynomials, and the calculation will be conducted and the necessary simplification steps will be taken, so to leave a polynomial function in its most compact form. Then, a polynomial graph will be provided

Then, once a valid polynomial expression has been provided, then you can click on the button below, the "Calculate" button, and all the required steps of the process will be shown.

Fractions algebra involves fraction conversion such as the use of common denominator, and the use of basic arithmetic rules. All in all, the process of the calculation can be laborious, although it can be done systematically, without much of a problem.

What is a polynomial function?

Polynomials, in the simplest explanation, are the functions that consist only of powers of \(x\), possibly multiplied by numerical constants, that are added (or subtracted) togheter. For example, \(p(x) = x^3 + 2x^2 + 1\) is a polynomial function, since it consists of the powers of \(x\) multiplied by constants, added together. In this case, \(1 = x^0\) so a constant is also a power of \(x\). :

In general, a polynomial function has the following form:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

with \(a_n \ne 0\). In this case, we say that the degree of the polynomial (or its order) is \(n\), which is the highest power present in the polynomial function.

Also, the coefficient \(a_n\) is called the leading coefficient, and \(a_n x^n\) is called the leading term. The leading coefficient and the degree of a polynomial will determine its end behavior (this is, the behavior when the absolute value of x is large).

What are the steps for working with a polynomial function?

• Step 1: Identify clearly the expression you want to work with, expand and simplify
• Step 2: Check whether the terms that involve the variable x only correspond to powers of x, otherwise you stop, it is not a polynomial
• Step 3: Make sure that all the powers of x are multiplied by constants (which could be '1'), and those terms appear as added or subtracted in the expression

It is important to make sure you have a polynomial function, so you can make sure you can apply results that are exclusive to polynomials, such as a the factor theorem, the remainder theorem and the rational zero theorem, which are extremely useful to find the solutions to polynomial equations, that are broadly used in different applications.

Also, the advantage of dealing with polynomial functions is that you can easily conduct division of polynomials, either by using long division, or synthetic division in case the divisor is linear.

Are there any important polynomial functions?

Indeed. There are the notorious polynomials of degree 2, which we call quadratic polynomials, which are extensively studied in basic Algebra. The reason for this is that they can be fully analyzed using precise formulas. For example, you have a formula for the vertex, and the famous quadratic formula is used to find roots for quadratic polynomials:

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

There is also the polynomials of degree 2, which we call cubic polynomials, which also have explicit formulas, but that are usually deemed to be more complex, and typically are not covered in basic algebra courses.

What do I know about the end behavior of a polynomial?

The end behavior of a polynomial will ultimately depend on the polynomial itself, but a few things can be said based on their degree

• Fact 1: For quadratic polynomials, the graph opens upward (if the leading coefficient is positive) or downward (if the leading coefficient is negative), and the function converges to infinite or minus infinity (depending on the sign of the leading coefficient) on both sides
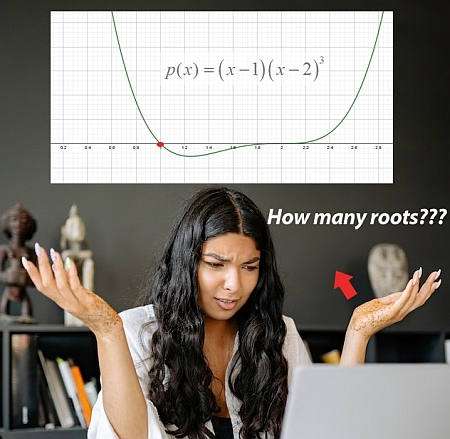
• Fact 2: For polynomials with degree that is odd (for example, with degree 3) will have at least one real root, and the function converges to infinite on one side, and to minus infinity on the other side
• Fact 3: For polynomials with degree that is even (for example, with degree 4), there won't be necessarily real roots (a point that he graph crosses in the x-axis), and the function converges to infinite or minus infinity (depending on the sign of the leading coefficient) on both sides

So, polynomials run large for large values of x, and whether their values are positive or negative for positive of x (in their end behavior) depends on the sign of the leading coefficient.

Tips: What are the benefits of using a polynomial functions calculator

Polynomial calculators can make sure you are arriving to the right answer. Indeed, polynomial calculations are not complicated, but they can be cumbersome and it is not hard to make mistakes.

Avoid algebraic mistakes by making sure you are checking your work with this calculator, so you can ensure of the consistency of the final answer and the steps used to get there.

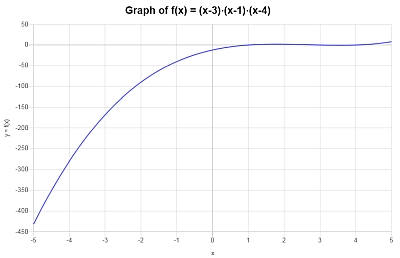
Example: Polynomial function

Calculate the following polynomial function \((x-3)(x-1)(x-4)\)

Solution: We are provided with the following polynomial expression that we need to calculate: \(\displaystyle (x-3)(x-1)(x-4)\).

The following calculation is obtained:

which concludes the process of polynomial simplification.

The following plot is obtained for \(\displaystyle x^3-8x^2+19x-12\) on the interval \([-5, 5]\):

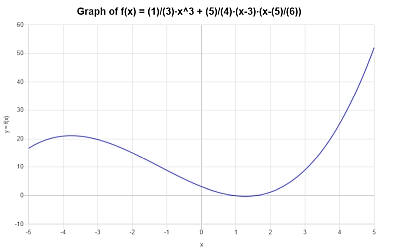
Example: Polynomial function calculation

Is this a polynomial function: \(\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)

Solution:

We are provided with the following polynomial expression that we need to calculate: \(\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\).

The following calculation is obtained:

which ends the simplification process.

Graphically, the following is obtained for the simplified function \(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\) on the interval \([-5, 5]\):

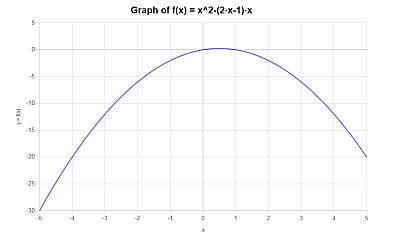
Example: Using a polynomial calculator

Calculate \( x^2 - (2x - 1)x \).

Solution:In this final example we have \(\displaystyle x^2 - (2x - 1)x \), which we need to simplify.

The following calculation is obtained:

which ends the simplification.

The following plot is obtained for \(\displaystyle -x^2+x\) on the interval \([-5, 5]\):

More Algebra Calculators

Polynomial functions are literally the center piece in Algebra. For basic applications, quadratic polynomials will play a key role and Economics, Physics and Engineering.

Polynomial functions have extremely powerful properties, especially involving the calculation of polynomial roots, which have a strong meaning in applications.