More about linear functions

This linear function calculator will allow you compute a linear function by providing certain required information about the function.

There are several ways you can do so. You can either (1) provide a linear equation in x and y that can be solved for y, or (2) provide directly the slope and y-intercept, or (3) you can provide the slope and a point where the line passes through, or (4) you can provide 2 points where the line passes through.

What information will you provide? It largely depend on what information you have available, and it will depend on the specific case.

One common case is to find a linear function that passes through two given points, but the other ways of determining the line are common too.

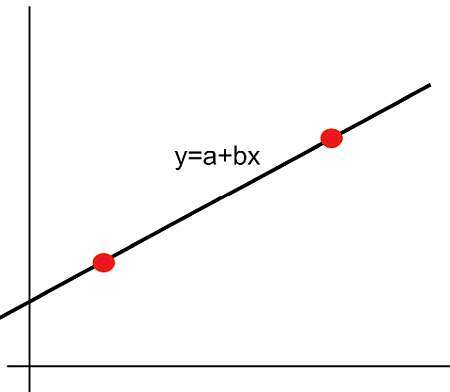
What is a linear function?

The answer depends on how many variables you are considering, but for one variable x, a linear function is a function of the form

\[f(x) = a + b x \]

Just a technicality, in more advanced math, this is a linear affine function, and it is not strictly linear unless a = 0, but that idea goes beyond the scope of this presentation. For us, \(f(x) = a + b x \) is a linear function in x.

The value of a in \(f(x) = a + b x \) is known as the y-intercept, and b is known as the slope. Sometimes you will see the convention \(f(x) = mx + n \), where m is the slope and n is the y-intercept.

But that is a name convention, you just need to recall that the constant that multiplies the variable x is the slope, and the other is the y-intercept. Why is that? Because when x = 0, we get \(f(0) = m \cdot 0 + n = n\), which indicates that n is precisely the why intercept.

What are the steps for computing a linear function?

• Step 1: Identify what type of information you have provided
• Step 2: If the information you have is a linear equation in x and y, you need to solve for y and then you automatically have the linear function setting f(x) = y
• Step 3: If you have the slope b and the y-intercept a, then the linear function is directly f(x) = a + b x
• Step 5: If you have two points \((x_1, y_1)\) and \((x_2, y_2)\) where the line passes through, then you can use the formula: \(\displaystyle f(x) = y_1 + \left(\frac{y_2-y_1}{x_2-x_1} \right)(x-x_1)\) for the linear function
• Step 6: If instead you have one point \((x_1, y_1)\) where the line passes through and the slope, then you can use the formula: \(\displaystyle f(x) = y_1 + m(x-x_1)\) for the linear function

The above list of steps is a comprehensive list and considers all possible cases. Ultimate, the simplest and less involved situation corresponds to the case where the slope and y-intercept are known, where we can compute the slope intercept form immediately, but that is not always the case.

What is the linear function formula

Ultimately, and regardless of the information you have provided, you can arrive to the linear function formula known as the slope-intercept form, which is:

\[y = a + bx \]

Now, since you are defining a function, you can also write \(f(x) = a + b x\).

What are the steps for finding the linear function formula?

• Step 1: Identify the information provided
• Step 2: Arrive at the corresponding formula y = a + bx, identifying the slope b and the y-intercept a
• Step 3: Replace y by f(x) and write f(x) = a + bx

Geometrically, the linear function graph will be a line that actually crosses the y-axis at the point (0, a), and the slope b will reflect the degree of inclination of the line.

Why is it useful to calculate linear functions?

The linear relationship between variables is very common in so many applications, so then it becomes indispensable to fully understand how linear functions work.

And we can also define linear functions for more variables, which make them an even more powerful object.

Example: Linear Function Calculator

Calculate the equation of the linear function that passes through the points: \( (\frac{22}{3}, \frac{7}{4})\) and \((-1, \frac{5}{6})\)

Solution: The main objective is to construct a linear function based on the information provided, if possible.

The information provided about the line is that the line passes through the points\(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\) and \(\displaystyle \left( -1, \frac{5}{6}\right)\)

Therefore, the first step consists in computing the slope. The formula for the slope is: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} \]

Now, by plugging the corresponding numbers is , we get that the slope is: \[\displaystyle b = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle \frac{5}{6} - \frac{7}{4}}{ \displaystyle -1 - \frac{22}{3}} = \frac{ \displaystyle \frac{5}{6}-\frac{7}{4}}{ \displaystyle -1-\frac{22}{3}} = \frac{11}{100}\]

So then, now we know that the slope is \(\displaystyle m = \frac{11}{100}\) and that the line passes through the point \(\displaystyle \left( \frac{22}{3}, \frac{7}{4}\right)\)

Hence, with the information we have, we can construct directly the point-slope form of the line, which is

\[\displaystyle y - y_1 = b \left(x - x_1\right)\]

and then plugging the known values of \(\displaystyle b = \frac{11}{100}\) and \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{22}{3}, \frac{7}{4}\right)\), we get that

\[\displaystyle y-\frac{7}{4} = \frac{11}{100} \left(x-\frac{22}{3}\right)\]

Now, we need to expand the right hand side of the equation by distributing the slope, so we get \[\displaystyle y = \frac{11}{100} x + \frac{11}{100} \left(-\frac{22}{3}\right) + \frac{7}{4}\]

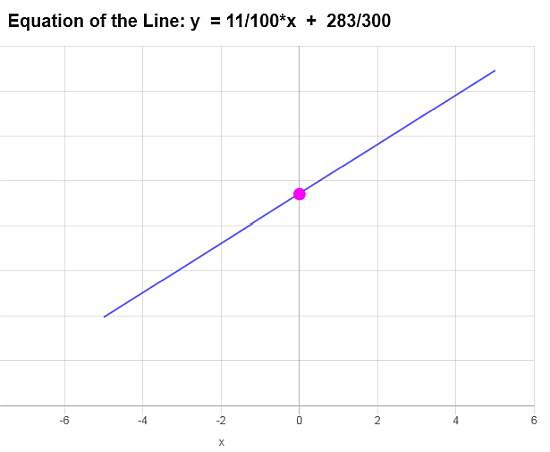
and simplifying we get that \[\displaystyle y=\frac{11}{100}x+\frac{283}{300}\]

Conclusion: Based on the data provided, we conclude that the equation of the line is \(\displaystyle f(x)=\frac{11}{100}x+\frac{283}{300}\), and it corresponds to a line with a slope of \(\displaystyle b = \frac{11}{100}\) and y-intercept of \(\displaystyle a = \frac{283}{300}\).

Based on this information, the graph is:

Example: Another Linear function calculation

Calculate the linear function associated to : \(\frac{1}{3}x + \frac{5}{4}y - \frac{5}{6} = 0\)

Solution:

Now for this example the way we have defined a linear function is via a general linear equation, given by:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

We can simplifying constants:

\[\displaystyle \frac{1}{3}x+\frac{5}{4}y-\frac{5}{6}=0\]

Now, putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x + \frac{5}{6}\]

Now, solving for \(y\), by dividing both sides of the equation by \(\frac{5}{4}\), the following is obtained

\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{5}{6}}{\frac{5}{4}}\]

and simplifying we finally get the following

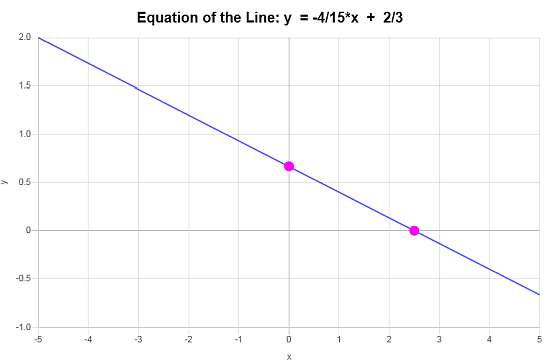
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{3}\]

Conclusion: Now we can say that based on the data provided, the conclusion is that that the equation of the line is \(\displaystyle f(x)=-\frac{4}{15}x+\frac{2}{3}\), and it corresponds to a line with a slope of \(\displaystyle b = -\frac{4}{15}\) and y-intercept of \(\displaystyle a = \frac{2}{3}\).

Based on this information, the graph is:

Example: More linear function calculators

Calculate the linear function with slope m = 0 and that crosses the y-axis at the point (0, 4).

Solution: In this case, we have given the slope, which is m = 0, and the y-intercept, which is (0, 4). Since the slope is 0, the line is horizontal, so in this case, the equation of the line is \(f(x) = 4\).

More linear function calculators

Interesting calculators are the slope calculator and y-intercept calculator. Also you may be interested in finding the perpendicular line to a given line.

Another common form for the line is the standard form, and you can certain convert from one form to the other.