More About this Linear Inequality Calculator

This calculator will provide you with the tools required to deal with linear inequalities. Specifically, you will be able to solve them and graph them, getting all the steps shown.

Linear inequalities like '2x + 3 < 1' or '3x + 2y <=1' are allowed, and then depending on the number of variables, you will get a suitable graph along with the steps that lead to the solution.

Once a valid linear inequality has been provided, then all you need to do is to click on "Solve" to get the process started. If there is something wrong or missing, the calculator will tell you about it.

These kinds of inequalities are the simplest kind you will find, and there are always relatively easy to solve. This type along with quadratic inequalities are among the only "easy" inequalities to solve.

What is a linear inequality?

A linear inequality is the simplest type of inequality, in which all the terms involved are linear or constant.

\[\displaystyle a x + b y \le 1\]

For example, the equation above is a linear equation with two variables. Technically speaking, we have polynomial inequality of degree 1, but that is a kind of overly complicated way of seeing it.

How do you Solve a Linear Inequality?

• Step 1: Put everything that contains the variable you want to solve for on one side, and the rest on the other side
• Step 2: Group and simplify the expression, so to reduce like terms
• Step 3: If a constant different than one is multiplying the variable you want to solve for, divide by it. One caveat: if you divide by a negative value, you need to change the direction of the inequality

One the main points to keep in mind, and that differentiate the processes of solving equations and inequalities is that when solving equations we can more freely multiply (or divide) by constants and nothing changes, whereas with inequalities we need to be more careful, as multiplying (or dividing) by negative constants changes the direction of the inequality.

What is the Most General Linear Inequality

The most general you can get with linear is

\[\displaystyle a x + bx \le c\]

but yet you may have '<' instead of '\(\le\)'. Or we could have

\[\displaystyle a x + bx \ge c\]

but you could also use '>' instead of '\(\ge\)'.

Similar to what happened with addition and subtraction, dividing fractions is just derived from the multiplication of fractions: To divide two fractions, you just multiply first one by the inverse fraction of the second one (the inverse fraction is obtained by swapping the numerator by the denominator in the fraction).

Applications

Linear inequalities find lots of applications in Math. A linear inequality is a type of weighted average, that is very suitable for all kind of mixing and assignment problems.

When dealing with word problems, usually you find linear equations, but it is not unusual to have to deal with linear inequalities as well.

One of the most well-known areas is Optimization and Linear Programming, in which linear inequalities play a crucial role, both with the Simplex method and with the Kuhn-Tucker conditions when dealing with a non-linear objective function.

Example: Solving inequalities

Solve the following linear inequality: \(\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}\)

Solution:

We need to put all terms of the inequality on one side:

\[\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0\]

Associated Auxiliary Equation

We need to solve:

\[\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0\]

Step 0: In this case, we first need to simplify the given linear equation, and in order to do so, we conduct the following simplification steps:

Solving the Linear Equation

Putting \(x\) on the left hand side and the constant on the right hand side we get

\[\displaystyle \frac{2}{3}x = -\frac{17}{12}\]

Now, solving for \(x\), by dividing both sides of the equation by \(\frac{2}{3}\), the following is obtained

\[\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}\]

and simplifying we finally get the following

\[\displaystyle x=-\frac{17}{8}\]

Therefore, the solving for \(x\) for given linear equation leads to \(x=-\frac{17}{8}\).

Critical Points

As expected for a linear inequality, there is only one critical point, which is \(-\frac{17}{8}\), from which we analyze the following intervals:

• For the interval \(\left(-\infty, -\frac{17}{8}\right)\): The left-hand side is negative, which means that \(\left(-\infty, -\frac{17}{8}\right)\) is part of the solution.

• For the interval \(\left(-\frac{17}{8}, \infty\right)\): The left-hand side is positive, which implies that \(\left(-\frac{17}{8}, \infty\right)\) is not a part of the solution.

Solution to the Inequality

Hence, it is found that the solution to the inequality is: \(x < -\frac{17}{8}\).

The expression the solution with interval notation, the solution is written as:

\[\left(-\infty,-\frac{17}{8}\right)\]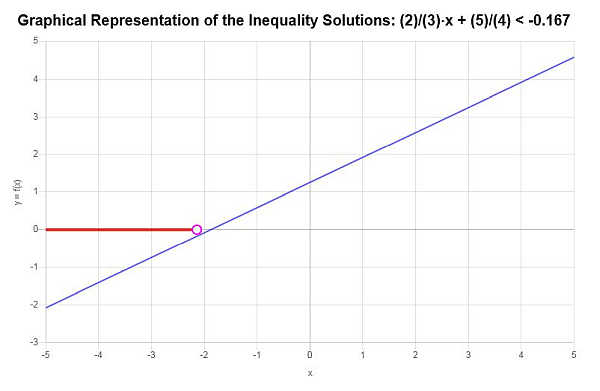

Example: More linear inequalities

Solve this 2-variable linear inequality: \(\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}\)

Solution:

We need to solve:

\[\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}\]

We have a linear inequality given, and we need to solve for the variable \(y\).

In this case, we solve for \(y\), so putting it one one side of the inequality and the rest to the other side we get:

\[\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}\]

In order to solve for \(y\), we divide both sides of the inequality by \(\frac{5}{4}\) so we get finally:

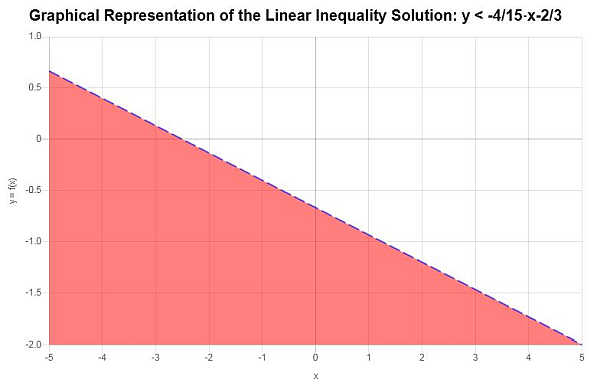
\[y < -\frac{4}{15}x-\frac{2}{3}\]

Linear Inequality Solution

Based on the inequality provided, after solving it for \(y\) we get:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

The graphical representation of the solution region is shown in the graph below:

More Algebra Calculators

Dealing with expression is crucial in Algebra. Expression simplification is the beginning of most mathematical processes, and you usually need to reduce things to its simplest expression.

Solving equations and also solving inequalities will remain at the core of most process, as one or the other will be at the center of mostly everything you do in Math.