Solvers Calculus

Chain Rule Calculator

Instructions: Use this Chain Rule calculator to compute the derivative of any composite function you provide, showing all the steps. Please type function you want to apply the Chain rule for in the form box below.

About the Chain Rule

This calculator will allow you to apply the chain rule to any composite function you provide. A composite function corresponds to the case when you evaluate a function inside of a function. In order for the Chain rule calculator to work, you need to provide a valid, differentiable composite function.

One example of a valid function would be f(x) = (sin(x))^2, where here we have the function 'x^2' that is being evaluated at another function, which is sin(x), forming a composite function.

Once a valid, differentiable function has been provided, the next thing you have to do is to click on the button that reads "Calculate", which then will set the calculations in motion and you will be shown all the steps.

The chain rule derivative is one of the most commonly used differentiation rule. This is because composition of function is one of the most natural way of constructing new functions based on elementary ones.

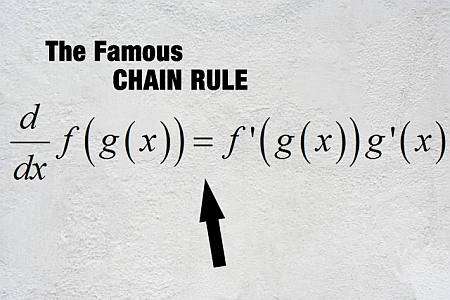
What is the Chain Rule

In simple words, the Chain Rule allows to differentiate composite functions, this is functions that are evaluated inside of other functions. So, say we have the function \(f(x)\) and \(g(x)\), and we know how to compute the derivative of these functions, which are \(f'(x)\) and \(g'(x)\).

Then, there is a Chain Rule formula that allows us to compute the derivative of the composite function \(f \circ g\), which is defined as \((f \circ g)(x) = f(g(x))\):

\[\displaystyle (f \circ g)'(x) = f'(g(x))g'(x)\]

Steps for using the Chain Rule

Step 1: Identify the external function f(x) and the internal function g(x)
Step 2: Make sure that f(x) and g(x) are valid, differentiable functions, and compute the corresponding derivatives f'(x) and g'(x)
Step 3: Use the formula (f \circ g)'(x) = f'(g(x))g'(x), which indicates that we evaluate the derivative of the external function at the internal function, and multiply that by the derivative of the internal function

Observe how the steps above use the idea of 'internal' and 'external' function. That is possibly not an standard term, but rather an idea that can help you identify the role played by each function when using the Chain Rule.

Chain Rule Applications

The Chain Rule is indeed and excellent tool to find derivatives, and normally will the key of any deriv calculator, along with all the other basic derivative rules. But the Chain Rule has a special interpretation in what is called Related Rates

To give context to the idea of related rates, let's start with a form of writing the Chain Rule that maybe lots of people will find easier to grasp:

\[\displaystyle \frac{dy}{dx} = \displaystyle \frac{dy}{dz} \cdot \frac{dz}{dx} \]

The above form of the Chain Rule is saying that if you \(y\) is a function of \(z\) and \(z\) is a function of \(x\), then ultimately \(y\) is a function of \(x\), and you can find the derivative of \(y\) with respect to \(x\) using the Chain Rule.

As you have probably suspected, \(y\) plays the role of \(f(x)\) (the 'external' function) and \(z\) plays the role of \(g(x)\) (the 'internal' function).

The above form of the Chain Rule links the rate of change of y with respect to x, with the rates of change of y with respect to z and that of z with respect to x, and hence the term 'related rates'.

This is extremely useful in practice. Example: the radius of a circle is increasing at a rate of 2 cm/sec, what is the rate of change of the area of the circle? So, you can either go and express the radius of the circle as a function of t, reflecting the fact that it increases at a rate of 2 cm/sec, OR, you can use the Chain Rule.

So you call A the area, r the radius, and t the time. What you need to calculate is \(\displaystyle \frac{dA}{dt}\), so you use the Chain rule directly, since you know \(A = \pi r^2\), and r'(t) = 2, so then

\[\displaystyle \frac{dA}{dt} = \displaystyle \frac{dA}{dr} \cdot \frac{dr}{dt} = 2\pi r \cdot 2 = 4 \pi r \]

Partial Derivative Chain Rule

Can you use the Chain rule with partial derivatives? Of course, partial differentiation is just like regular differentiation, only that the other variables are assumed to be constant, so then the usual derivative rules apply.

So then, the ideal of multivariable chain rule applies, only that one variable varies at a time.

Chain Rule integration

The Chain Rule in the sense of what it does not apply as a derivative tool, but instead it becomes an invaluable integration tool for substitutions and change of variables.

It can be conceived as a sort of reverse chain rule of sorts.

Example: Using the Chain Rule

Calculate the derivative of the function: \(f(x) = \sin(\cos(x)) \)

Solution: Consider the function \(\displaystyle f(x)=\sin\left(\cos\left(x\right)\right)\). This function corresponds to the composition of two functions: sin(x) and cos(x), for which reason the Chain Rule would apply in this case.

\( \displaystyle \frac{d}{dx}\left(\sin\left(\cos\left(x\right)\right)\right)\)

So we start using the Chain Rule: \(\frac{d}{dx}\left( \sin\left(\cos\left(x\right)\right) \right) = \frac{d}{dx}\left(\cos\left(x\right)\right)\cdot \cos\left(\cos\left(x\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\cos\left(x\right)\right)\cdot \cos\left(\cos\left(x\right)\right)\)

Next, directly differentiating: \(\frac{d}{dx}\left( \cos\left(x\right) \right) = -\sin\left(x\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(-\sin\left(x\right)\right) \cos\left(\cos\left(x\right)\right)\)

which then leads to

\( \displaystyle = \,\,\)

\(\displaystyle \left(-\sin\left(x\right)\right)\cos\left(\cos\left(x\right)\right)\)

Finally, the following is found

\( \displaystyle = \,\,\)

\(\displaystyle \left(-1\right)\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\)

What is the conclusion: We can conclude that the derivative we are looking for is:

\[f'(x) = -\cos\left(\cos\left(x\right)\right)\sin\left(x\right)\]

and this concludes the calculation.

Chain Rule Example

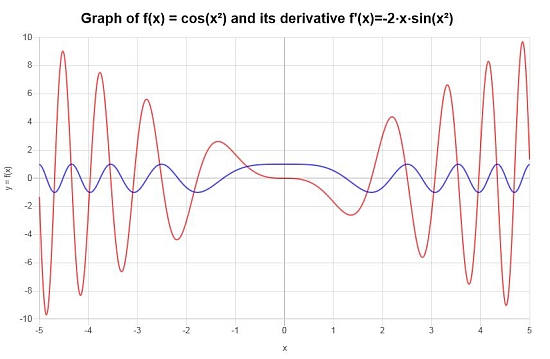
Using the chain rule, and any other derivative rules, calculate: \(\displaystyle \frac{d}{dx} \left( \cos(x^2) \right)^2\)

Solution: In this example we have the function \(\displaystyle f(x)=\cos\left(x^2\right)\), which corresponds to a compounded function, which indicates that the Chain Rule is the right derivative rule to start with (other rules will be needed along the calculations)

\( \displaystyle \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)

First, we use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\)

We can use the Power Rule for polynomial terms in this case: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \left(-\sin\left(x^2\right)\right)\)

and then we find

\( \displaystyle = \,\,\)

\(\displaystyle 2x\cdot \left(-\sin\left(x^2\right)\right)\)

Now, simply reorganizing terms

\( \displaystyle = \,\,\)

\(\displaystyle -2x\sin\left(x^2\right)\)

Final Derivative: The conclusion is that the derivative of the function provided is given by:

\[f'(x) = -2x\sin\left(x^2\right)\]

We can construct the following graphical depiction on the interval \([-5, 5]\):

Example: Another chain rule calculation

Compute the derivative of \( f(x) = x^2 \sin(x^2)\) by using the chain rule.

Solution:

The following function has been provided: \(\displaystyle f(x)=x^2\sin\left(x^2\right)\), for which we need to compute its derivative.

The function came already simplified, so we can proceed directly to compute its derivative:

\( \displaystyle \frac{d}{dx}\left(x^2\sin\left(x^2\right)\right)\)

We can use the Product Rule: \(\frac{d}{dx}\left( x^2\sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \sin\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \sin\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\sin\left(x^2\right)\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( \sin\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \cos\left(x^2\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle \left(2x\right) \sin\left(x^2\right)+x^2 \cdot 2x\cdot \cos\left(x^2\right)\)

so then we get that

\( \displaystyle = \,\,\)

\(\displaystyle x^2\cdot 2x\cos\left(x^2\right)+2x\sin\left(x^2\right)\)

Putting the integers together and grouping the terms with \(x\) in the term \(x^2\cdot 2x\cos\left(x^2\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x^3\cos\left(x^2\right)+2x\sin\left(x^2\right)\)

So then we get

\( \displaystyle = \,\,\)

\(\displaystyle 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\)

What is the final conclusion: The final conclusion is that the derivative we are looking for is given by:

\[f'(x) = 2\left(x^2\cos\left(x^2\right)+\sin\left(x^2\right)\right)x\]

Graphically we have:

Other derivative calculators

Certainly using a derivative calculator will make things easier when dealing with rather complicated functions. The process of differentiating gets large facilitated by the use of common, easy to remember derivative rules, including the product rule, the quotient rule and the chain rule.

These rules will help you deal with every differentiable function, but the algebraic process of the calculation and simplification may not be necessarily easy.