More about this area to diameter calculator

This calculator show you all the calculations required to go from the area of a circle to its diameter, showing you all the steps of the process

All you need to do is provide a valid numeric expression that is positive. For example, you can provide 3/4, or 3, or sqrt(3) or a compound expression, providing that is valid and it is positive.

Once you provide a valid area is provided, you just need to click on "Calculate", and the solution with its steps will be displayed.

The process of going from the area to the diameter is simple and based on using one area formula, but it is crucial that the provided area is positive.

How to find the diameter from the area?

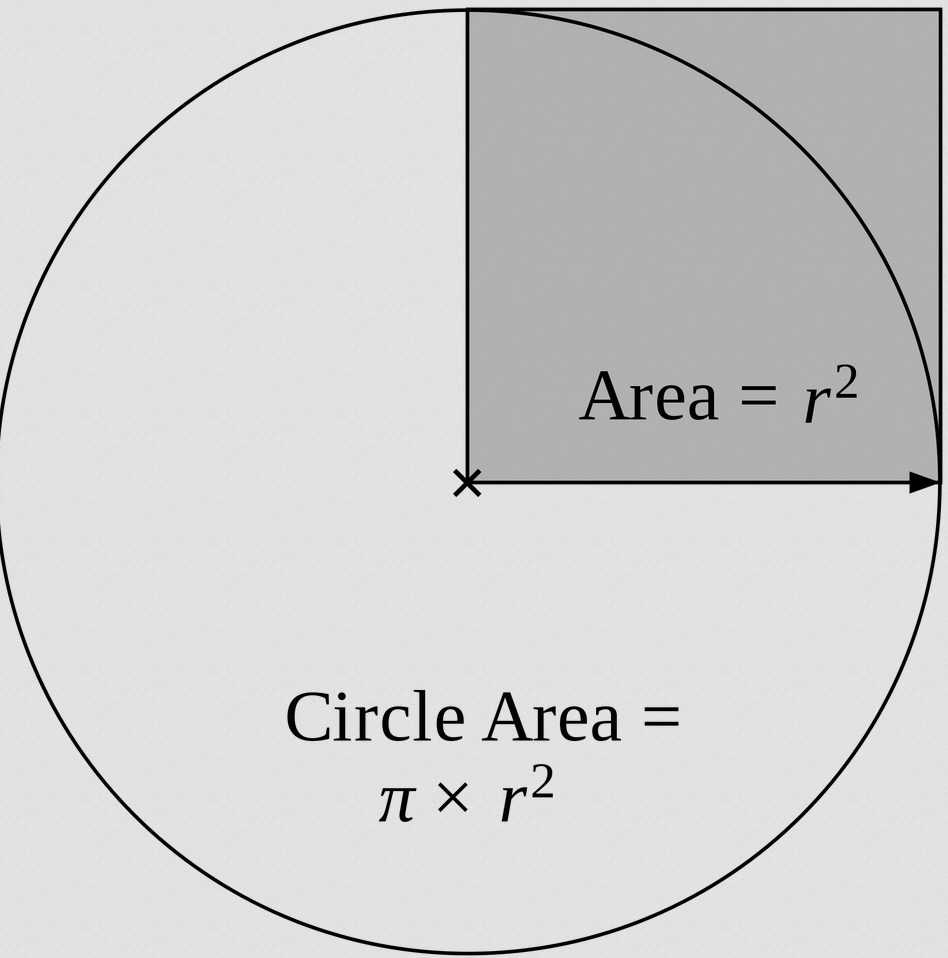
Let us recall that the traditional area formula is

\[A = \displaystyle \pi r^2 \]

and solving for r leads to:

\[\Rightarrow r^2 = \displaystyle \frac{A}{\pi} \] \[\Rightarrow r = \displaystyle \sqrt{ \frac{A}{\pi}} \]

But we need to recall that r = d/2, so we get

\[\displaystyle \frac{d}{2} = \displaystyle \sqrt{ \frac{A}{\pi}} \]

which finally leads to the area to diameter formula:

\[d = \displaystyle 2 \sqrt{ \frac{A}{\pi}} \]

What are the steps for finding the diameter?

• Step 1: Identify the area that is given. If circumference is given instead you need to use the formula for the circumference to diameter, which is different one
• Step 2: Once you have a valid area A, you need to plug it into the formula: \(d = \displaystyle 2 \sqrt{ \frac{A}{\pi}}\)
• Step 3: Make sure that if the area A is passed with length units, you pass them to the diameter too

For example, if the area A is given as 3 cm², then the diameter will be measured in cm.

Normally in Geometry and Algebra the use of length is less common, and perhaps more than being less common, it is assumed to be clear and unambiguous, which is usually the case except when conversion of units is needed.

Why would care about dealing with areas and diameters?

The concepts of areas and diameters are crucial in math, and it is only natural to be interested in the relationship. It is true that there is a clear link between area and radius and that perhaps should be enough, but the diameter has lots of interest in its own right.

Areas, circumferences, radius and diameter are central components in Math, and it is relevant to solve equations that link them.

Example: Calculating the diameter

Assume that the area of a circle is \(A = 4\pi\), find its diameter d.

Solution: We know, based on the setting of the problem that the area is known to be \(A = 4\pi\).

All we have to do now is to simply plug in this value of A into the formula:

\[d = \displaystyle 2 \sqrt{ \frac{A}{\pi}} = \displaystyle 2 \sqrt{ \frac{4\pi}{\pi}} = 4 \]

which concludes the calculation.

Example: More areas and diameters

A sector of a circle with an angle of 60^o has an area of \(\frac{3}{2}\pi\), find the diameter.

Solution:We know that 60^o represents 1/6 of the full circle. Since the area of the sector is proportional to its angle, the area of the full circle is therefore \(A = 6\cdot \frac{3}{2}\pi = 9\pi\).

All we have to do now is to plug in this value of A into the formula:

\[d = \displaystyle 2 \sqrt{ \frac{A}{\pi}} = \displaystyle 2 \sqrt{ \frac{9\pi}{\pi}} = 6 \]

which concludes the calculation.

Example: Negative areas?

Given and area of A = -3, can you compute the diameter?

Solution: No, you cannot. In order to compute the diameter from the area, you need a positive area A. Or if the area A = 0, then the diameter is d = 0 as well. But you cannot do the calculation with a negative area.

More circle calculators

Calculating circumferences and areas is a basic skill and Geometry, and it is important to know how they are inter-related.

Also, you may try our circle equation calculator, or you can specifically get the circle in standard form or in general form.

Expressing the equation of a circle in different forms does not change the circle's geometric properties, such as its area and circumference, but it can be practical in many applications because of its algebraic manipulations.