More about Function Composition

This calculator will allow you calculate a function composite \(f \circ g\) based on two functions \(f\) and \(g\) that you provide. Notice that in general \(f \circ g\) is not the same as \(g \circ f\) so the order is relevant.

When calculating the composition \(f \circ g\), there is one internal function \(g\) and one external function \(f\), and you change the order, very often the outcome varies.

Observe that \(f\) and \(g\) need to be validly defined functions, like for example \(f(x) = \sqrt{x}\) and \(g(x) = 2x+1\), so then we would have that \((f \circ g)(x) = f(g(x)) = \sqrt{2x+1}\) .

What is a composite function?

In order to form a composite function, you evaluate one function inside of another function. Let \(f\) and \(g\) be functions, the composite function is defined as

\[\displaystyle (f \circ g)(x) = f(g(x)) \]

What are the steps for finding the composite function?

• Step 1: Identify the functions f and g you will do function composition for
• Step 2: Clearly establish the internal and external function. In this case we assume f is the external function and g is the internal formula
• Step 3: The composite function is defined as (f◦g)(x) = f(g(x))

You can simplify the resulting output of f(g(x)), and in fact, the calculator will simplify it for you. One main point of importance is to realize you may need to restrict the domain of the composite function so it is well defined.

What is a fog calculator

In this case, fog is not the fog that you know, it is referring to the composition of f and g, written as \(f \circ g\).

Composition of functions will be as algebraically involved as the complexity of the composing functions. This is, composing simple functions will lead to a simple composite function, that is easy to calculate.

Using this composite calculator

The advantage of using this composite calculator is that you will get the composite function calculated and simplified into its simplest terms, but you will also get the composite function graphed.

Composite function chain

Composition can be applied to more than two functions. For example, consider the functions \(f\), \(g\) and \(h\). The chain composition is defined as

\[\displaystyle (f \circ g \circ h)(x) = f(g(h(x))) \]

where the order in which you compound the expressions is relevant.

Domain of composite function calculator

Notice that the domain of a composite function can be different than that of the two original functions. For example, let's see again the case of \(f(x) = \sqrt{x}\) and \(g(x) = 2x+1\). The domain of f is \([0, \infty)\) and the domain of g is \((-\infty, \infty)\), but since \((f\circ g)(x) = \sqrt{2x+1}\), the domain of \(f\circ g\) is \([-\frac{1}{2}, \infty)\).

Example: Function composition

Calculate and graph: \((f \circ g)(x)\) for \(f(x) = \sqrt{x}\) and \(g(x) = 2x-1\).

Solution: The following functions has been provided: \(\displaystyle f(x)=\sqrt{x}\) and \(\displaystyle g(x)=2x-1\), for which we need to calculate the composite function \(f \circ g\).

By definition, the composite function \(f \circ g\) is defined as:

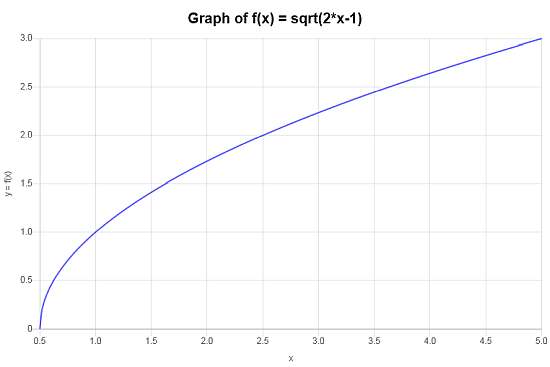
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \sqrt{2x-1} \end{array}\]

There is nothing to simplify in this case, and then, the composite function we are looking for is \(f \circ g(x)=\sqrt{2x-1}\).

The following plot is obtained for the compounded function \(f \circ g(x)=\sqrt{2x-1}\) on the interval \([-5, 5]\):

Example: Composite Function calculation

Calculate and graph: \((f \circ g)(x)\) for \(f(x) = x^{3/2}\) and \(g(x) = x+2\). Is \((f \circ g)(x)\) the same as \((g \circ f)(x)\) in this case?

Solution:These are the function we need to compound: \(\displaystyle f(x)=x^{3/2}\) and \(\displaystyle g(x)=x+2\).

By definition, the composite function \(f \circ g\) is defined as:

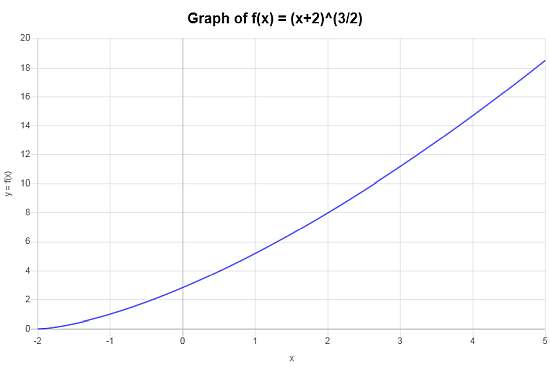
\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x+2\right)^{3/2} \end{array}\]

There is nothing to simplify in this case, and then, the composite function we are looking for is \(f \circ g(x)=\left(x+2\right)^{3/2}\).

The following graph is obtained for the compounded function \(f \circ g(x)=\left(x+2\right)^{3/2}\) on the interval \([-5, 5]\):

Example: Composite Function calculation example

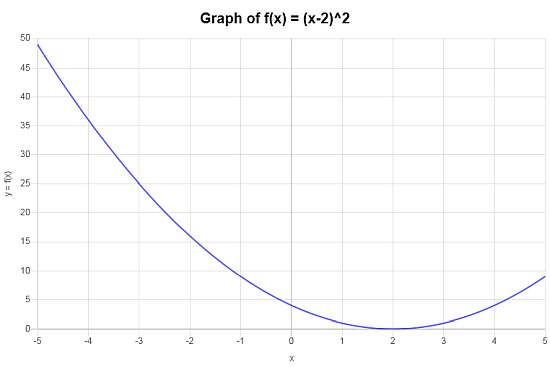
Find \((f \circ g)(x)\) for \(f(x) = x^2\) and \(g(x) = x-2\) and graph the composite function.

Solution:In this example we need to work with \(\displaystyle f(x)=x^2\) and \(\displaystyle g(x)=x-2\), which requires us to compute the composite function. \(f \circ g\).

Using the definition, the composite function \(f \circ g\) is defined as:

\[\begin{array}{ccl} f \circ g & = & f(g(x)) \\\\ & = & \left(x-2\right)^2 \end{array}\]

The above expression needs to be simplified, and the steps are as follows:

So then, after simplifying, the composite function that is obtained is \(f \circ g(x)=x^2-4x+4\).

The compounded function \(f \circ g(x)=x^2-4x+4\) leads to the following plot on the interval \([-5, 5]\):

More Algebra calculators

Functions are one of the main elements in Algebra and Calculus. And the reason for that is that it embodies a way to establish a relationship between two variables x and y.

Lots of applications depend on operations you perform and also the graph of a function, which contains all the information 'stored' in the function.