Über polynomgleichungen

Verwenden Sie diesen Taschenrechner, um die Polynomgleichungen zu lösen und alle Schritte des Prozesses anzuzeigen.Die von Ihnen bereitgestellte Gleichung kann links und rechts von der Gleichung polynomiale Begriffe haben.

Sie können beispielsweise eine Gleichung wie 3x^3 - 2x = 1 + x bereitstellen, die aus dem Versuch abgeleitet werden kann, den Schnittpunkt der Graphen einer Kubik- und einer linearen Funktion zu finden.Jede Polynomgleichung wird mit Ganzzahl- oder Bruchkoeffizienten oder einem gültigen numerischen Ausdruck ausgesetzt.

Sobald eine Polynomgleichung in das Formularfeld eingegeben wurde, müssen Sie auf "Berechnen" klicken, die alle Schritte des Prozesses und der Lösungen anzeigen.

Ein Haftungsausschluss, nicht alle Polynomgleichungen können mit grundlegenden Werkzeugen gelöst werden.Es gibt keine systematische Formel, um mit der Polynomgleichung von Grad 5 oder höher umzugehen.Wir befassen uns auch mit der zusätzlichen Schwierigkeit, dass die Lösungen für eine Polynomgleichung komplexe Zahlen sein können.

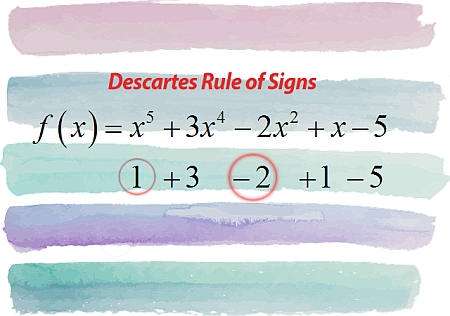
Was ist eine polynomgleichung

Eine Polynomgleichung ist in einfachen Worten eine Gleichung, in der beide Seiten Polynome enthalten.Mathematisch ist eine Polynomgleichung von der Form:

\[\displaystyle p(x) = q(x) \]

wobei \(p(x)\) und \(q(x)\) Polynome sind. Zum Beispiel ist \(3x+1 = x^2-2\) eine Polynomgleichung, aber \(\sin(3x+1) = x^2-2\) ist keine.

Was sind die schritte zum lösen von polynomgleichungen?

• Schritt 1: Identifizieren Sie die Gleichung, mit der Sie arbeiten möchten, und geben Sie klar die Begriffe auf der linken und rechten Seite an und stellen Sie sicher, dass es sich um Polynome handelt
• Schritt 2: Vereinfachen Sie jede Seite so weit wie möglich.Geben Sie alle Bedingungen an einer der Seiten an den anderen weiter (wenn beide Seiten Begriffe haben)
• Schritt 3: Jetzt haben Sie eine Polynomgleichung, die so eingestellt ist, dass sie Null sind. Daher müssen wir die Wurzeln des Polynoms finden
• Schritt 4: Wir versuchen mit möglichen rationalen Wurzeln, polynomialer Aufteilung für Reduktion und quadratische Formel, wie in der gezeigt Polynom -Null -Rechner Wenn möglich die Lösungen zu finden

Sie werden feststellen, dass die Lösung von Polynomgleichungen für alle Fälle alles andere als trivial ist, da das Finden von Wurzeln eines Polynoms alles andere als trivial ist.Sicherlich können einige spezifische Beispiele sehr einfach sein, aber wenn der Exponent der beteiligten Polynome groß ist, kann der Prozess sehr schwierig oder einfach unmöglich sein.

Sind quadratische gleichungen auch polynomgleichungen?

Ja in der Tat!Eine quadratische Gleichung ist eine Gleichung mit einem Polynom von Grad 2 auf der linken Seite und 0 (was auch ein Polynom ist) auf der rechten Seite, so dass sie auf die Definition passt.

In Der Tat, quadratische Gleisungen sind ungefähr das Beste, was wir mit einfachen Werkzeugen lösen können.Obwohl es Formeln für kubische und quartische Gleichungen gibt, gibt es keine allgemeine Formel für Abschluss 5 oder höher.Dann verlassen wir uns auf Computer, um numerische Näherungen oftmals zu finden.

Außerdem kann der Exponent des Polynoms eine Gleichung schwer zu lösen, sondern auch umständliche Polynomkoeffizienten können die Dinge sicherlich erschweren.

Wie hängen polynome mit polynomgleichungen zusammen?

Es gibt verschiedene Möglichkeiten, es zu sehen, aber eine Möglichkeit besteht darin, zu bemerken, dass wir durch den Versuch, den Schnittpunkt verschiedener Polynome zu finden, tatsächlich eine Polynomgleichung lösen.Es gibt also eng verwandte Probleme.

Beispiel: polynomgleichungen lösen

Berechnen Sie die folgende Polynomgleichung: \(x^2 = x^3\)

Lösung: Wir müssen \(x^2 = x^3\) lösen, also führen wir \(x^3\) auf die andere Seite, so dass wir erhalten

\[ x^2 - x^3 = 0\]

und Factoring führt zu:

\[ x^2(1 - x) = 0\]

Dann gibt es also zwei Lösungen: \(x_1 = 0\) (mit der Vielfachheit 2), und \(x_2 = 1\).

Beispiel: polynomgleichungen lösen

Wie lauten die Lösungen der folgenden Gleichung? \(\frac{2}{3} x^2 + \frac{5}{4} x = \frac{1}{3} x^2 - \frac{5}{6}\)

Lösung: Wir müssen die folgende Gleichung lösen:

\[\displaystyle \frac{2}{3}x^2+\frac{5}{4}x=\frac{1}{3}x^2-\frac{5}{6}\]

Erstschritt: In diesem Fall müssen wir zunächst die gegebene Gleichung \(\displaystyle \frac{2}{3}x^2+\frac{5}{4}x=\frac{1}{3}x^2-\frac{5}{6} \) vereinfachen, indem wir alle Terme auf eine Seite der Gleichung setzen, so dass wir erhalten:

Nach der Vereinfachung müssen wir also die folgende Polynomgleichung der Ordnung \(2\) lösen:

\[\displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = 0\]

Beachten Sie, dass der Grad des gegebenen Polynoms \(\displaystyle deg(p) = 2\) ist, sein führender Koeffizient \(\displaystyle a_{2} = \frac{1}{3}\) und sein konstanter Koeffizient \(\displaystyle a_0 = \frac{5}{6}\).

Wir müssen die folgende quadratische Gleichung \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6}=0\) lösen.

Für eine quadratische Gleichung der Form \(a x^2 + bx + c = 0\) werden die Wurzeln mit Hilfe der folgenden Formel berechnet:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall ist die Gleichung, die wir lösen müssen, \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = 0\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = \frac{5}{6}\]

Erstens werden wir die Diskriminanz berechnen, um die Art der Wurzeln zu bewerten.Die Diskriminierung wird berechnet als:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{5}{4}\right)^2 - 4 \cdot \left(\frac{1}{3}\right)\cdot \left(\frac{5}{6}\right) = \frac{65}{144}\]

Da die Diskriminante in diesem Fall \(\Delta = \displaystyle \frac{65}{144} > 0\) ist, die positiv ist, wissen wir, dass die Gleichung zwei verschiedene reelle Wurzeln hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{65}{144}}}{\frac{2}{3}}\]

Also finden wir das:

\[ x_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{65}{144}}=-\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\cdot\frac{1}{12}\sqrt{65}=-\frac{5}{4}\cdot \frac{3}{2}-\frac{\frac{1\cdot 3}{2}\cdot 1}{12}\sqrt{65}=-\frac{15}{8}+1\cdot \left(-\frac{1}{8}\right)\sqrt{65}=-\frac{15}{8}-\frac{1}{8}\sqrt{65} \] \[x_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{65}{144}}=-\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\cdot\frac{1}{12}\sqrt{65}=-\frac{15}{8}+1\cdot \frac{1}{8}\sqrt{65}=-\frac{15}{8}+\frac{1}{8}\sqrt{65}\]

In diesem Fall hat die quadratische Gleichung \( \displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = 0 \) zwei reelle Wurzeln, also:

\[\displaystyle \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = \frac{1}{3} \left(x+\frac{1}{8}\sqrt{65}+\frac{15}{8}\right)\left(x-\frac{1}{8}\sqrt{65}+\frac{15}{8}\right)\]

das ursprüngliche Polynom wird also als \(\displaystyle p(x) = \frac{1}{3}x^2+\frac{5}{4}x+\frac{5}{6} = \frac{1}{3} \left(x+\frac{1}{8}\sqrt{65}+\frac{15}{8}\right)\left(x-\frac{1}{8}\sqrt{65}+\frac{15}{8}\right) \) faktorisiert, womit die Faktorisierung abgeschlossen ist.

Schlussfolgerung : Die Lösungen der Polynomgleichung, die mit Hilfe des Faktorisierungsverfahrens gefunden wurden, sind \(-\frac{1}{8}\sqrt{65}-\frac{15}{8}\) und \(\frac{1}{8}\sqrt{65}-\frac{15}{8}\) .

Mehr polynomrechner

Polynomegleichungen erscheinen in Algebra so natürlich, dass sie eines der wichtigsten Themen in Algebra sind.Wenn Sie nach dem Schnittpunkt von zwei suchen Parabel , du wirst brauchen Ein Polynomgleung Lösen nur um eine Situation vieler zu erwähnen.

Der einfachste Fall einer Polynomgleichung ist der Fall, dass man eine Lineare Gleisung , was in der Tat ein trivialer Fall ist. Alles, was nicht linear ist, erfordert eine ganze Menge mehr Arbeit.

Die Lösung der Polynomgleichung ist insbesondere bei höher Polynomgrad .In der Tat besteht eine gewisse Möglichkeit, dass Sie nicht in der Lage sind, die gesamte Lösung einer bestimmten Gleichung manuell (oder eine Lösung für diese Angelegenheit) zu finden.

Die beste manuelle Alternative besteht darin, alle Polynombegriffe auf der einen Seite zu gruppieren, um sie auf zu reduzieren Finding der Nullen Einen Polynoms .Dann verwenden wir die quadratische Formel, wenn möglich, und versuchen, die Reihenfolge des Polynoms durch zu verringern Polynomabelung und die Faktorsatz .