Polynom -langstuferechner

Dieser Taschenrechner hilft Ihnen bei der Durchführung einer langen Abteilung zwischen zwei gegebenen Polynomen.Zu diesem Zweck müssen Sie zwei gültige Polynomausdrücke bereitstellen.Diese Polynome sind möglicherweise bereits vereinfacht oder nicht, und der Taschenrechner vereinfacht sie, wenn sie es benötigen.

Wann Polynome Teilen Sie müssen zwei Polynome bereitstellen, eine, die Sie teilen werden, was als Dividende bezeichnet wird, und der andere ist der Divisor.

Sobald Sie zwei gültig angeben Polynom Der nächste Schritt wäre, auf die Schaltfläche "Berechnen" zu klicken, die die gesamte entsprechende Berechnung zeigt, die für die gewünschte lange Abteilung zwischen den bereitgestellten Polynomen erforderlich ist.

Der Prozess der Durchführung einer Teilung von Polynomen mit der Lange Divisionsmethode ist eine relativ einfache Methode, die jedoch einen sehr organisierten Ansatz erfordert, um nicht verloren zu gehen.Normalerweise funktioniert es am besten mit einem tabellarischen Ansatz, um die entsprechenden Schritte anzuzeigen.

Ein einfacherer Ansatz wird mit verwendet Synthetische Abteilung , aber das gilt nur dann, wenn der Divisor einen Abschluss hat, so dass er eine begrenztere Reichweite hat

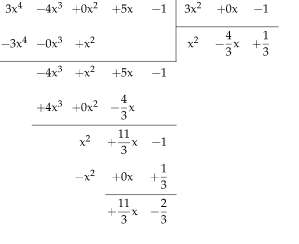
Was ist ein polynom?

Ein Polynom ist eine Art einfacher Ausdruck, der sich mit Summen und Subtraktionen kombiniert, die die Ganzzahlmächte einer bestimmten Variablen x (oder welcher variablen Namen, der ausgewählt wird), möglicherweise von Konstanten multipliziert.

Zum Beispiel ist der Ausdruck \(p(x) = 2x^2 + x + 1\) eine Kombination der Begriffe \(2x^2\), \(x\) und \(1\) mit Ergänzungen von X (Beachten Sie, dass 1 eine Kraft von x ist, als\(x^0 = 1\).

Andererseits ist \(f(x) = 2x^2 + \sin(x) + 1\) kein Polynom, da der Begriff \(\sin(x)\) keine Leistung von x ist.

Polynomoperationen

Polynome können ähnlich wie Zahlen mit betrieben werden Addition, Unterhandel, Multiplikation und Spaltungen von Polynomen .Ergänzungen und Subtraktionen sind auf sehr intuitive Weise einfach zu tun.Wenn Sie beispielsweise zwei Polynome haben, \(p(x) = 2x+1\) und \(q(x) = x^3 + 2x+ 3\) wird das Hinzufügen des Polynoms erreicht, indem die Begriffe wie buchstäblich hinzugefügt werden wie

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

Für Subtraktionen subtrahieren Sie auch die entsprechenden Begriffe des Subtrahierens des Polynoms.Wenn Sie beispielsweise zwei Polynome haben, \(p(x) = 2x+1\) und \(q(x) = x^3 + 2x+ 3\), ist die Subtrahiere wie möglich wie

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

Die Multiplikation ist komplizierter, da Sie mithilfe der Verteilungseigenschaft die Begriffe mit den Multiplikationen überschreiten müssen:

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

Die Teilung ist etwas komplizierter, da es sich um die Idee handelte, dass ein Polynom möglicherweise nicht teilt Exakt ein weiteres Polynom.Mathematisch, wenn wir zwei Polynome haben \(p(x)\) und \(s(x)\) und wir wollen \(p(x)\) von \(s(x)\) teilen, suchen wir nach einem Quotienten \(q(x)\) und einen Rest\(r(x)\) (beide Polynome), die die Eigenschaft haben, die \(p(x)= q(x)\cdot s(x) + r(x)\) mit der Bedingung, dass die Polynomgrad \(r(x)\) ist geringer als der Grad von \(s(x)\).Dies wird normalerweise die genannt Euklid -Queretzung .

Die lange divisionsmethode

Die Long Division -Methode ist also eine systematische Methode, um mit zwei Polynomen zu beginnen, die wir teilen möchten \(p(x)\) und \(s(x)\), also finden wir Quotient \(q(x)\) und ein Rest \(r(x)\) in solchenein Weg das

\[p(x)= q(x)\cdot s(x) + r(x)\]

Dieser Algorithmus ist äußerst nützlich, und obwohl das Problem im Aussehen einfach erscheint, ist es nicht schwierig, sich zu verlieren, wenn sie keinen systematischen Ansatz verwenden, der garantiert zum erforderlichen Quotienten und Rest ankommt.

Was sind die schritte für eine lange abteilung?

• Schritt 1: Identifizieren Sie die beiden Polynome p (x) und s (x), die Sie trennen und p (x) als Dividende und S (x) als Divisor identifizieren und identifizieren möchten
• Schritt 2: Überprüfen Sie den Grad der Dividende P (x) gegen den Grad von S (x).Wenn der Grad von S (x) größer ist als der Grad von p (x), haben wir, dass der Rest die Dividende P (x) selbst ist und der Quotient Null ist: q (x) = 0, und Sie sind fertig
• Schritt 3: In diesem Fall gehen wir davon aus
• Schritt 4: Wir müssen einen iterativen Prozess durchführen, um einen vorübergehenden Rest zu finden, bis wir zum Rest angekommen sind, der einen Grad weniger als den Grad von S (x) hat.
• Schritt 5: Der vorübergehende oder vorläufige Rest wird jedes Mal aktualisiert, indem er zuerst das Verhältnis zwischen der höchsten Laufzeit des aktuellen restlichen Restes und dem Teil der Divisoren (x) ermittelt hat.Dieses Verhältnis (das ein Leistungsbegriff ist) multipliziert dann S (x), und das Ergebnis dieser Multiplikation wird vom aktuellen restlichen Rest abtrahiert, was zu einem aktualisierten Rest führt
• Schritt 6: Dieser Prozess wird fortgesetzt, bis der Rest einen Grad hat, der niedriger ist als der von S (x).In jedem Schritt der Iteration wird der Grad des vorübergehenden Restes um mindestens 1 reduziert, sodass der Prozess garantiert endet

Am Ende der Prozess von Zwei Polynome Teilen wird reduziert, um Multiplikationen zu berechnen, sind Summen von Polynomen, was mit Zahlen so gut wie passiert.Die Long Division -Methode für Polynome ist die Erweiterung der Art und Weise, wie wir Zahlen an Polynome teilen.

Wie hängt eine lange teilung mit dem auffinden von wurzeln einer polynomgleichung verbunden?

Angenommen, P (x) ist die Dividende, die Sie teilen möchten, und S (x) ist der Divisor.Nach der Long Division -Methode können Sie einen Quotienten Q (x) und einen Rest r (x) finden, damit:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

Aber manchmal kommt es vor, dass der Rest r (x) = 0 ist, und in diesem Fall sagen wir, dass s (x) p (x) teilt (oder es genau teilt).Also, wenn r (x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

Dies weist darauf hin, dass wir, um Wurzeln von P (x) = 0 zu finden, q (x) = 0 und s (x) = 0, getrennt zu lösen, die einfachere Gleichungen sind, die zu lösen sind.

Vorteile dieses langen abteilungsrechners

Wie ich bereits erwähnt habe, ist Long Division nicht zu schwer, erfordert jedoch einen systematischen Ansatz.Ein großer Vorteil der Verwendung a Fähigitungsreichner Wie dieses ist, dass Sie alle Schritte des angezeigten Prozesses erhalten

Es ist möglicherweise nicht wichtig zu wissen, wie man die Schritte selbst durchführtSie die Antwort, ohne die Schritte anzuzeigen.

Ein langer Abteilungsrechner mit Schritten, die alle Arbeiten zeigen, stellt sicher, dass Sie eine klare Vorstellung davon bekommen, was mit der Berechnung passiert.

Beispiel: berechnung der teilung von polynomen

Berechnen Sie die Teilung der folgenden Polynome: \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) und \(s(x) = x+3\).

Lösung: Das folgende Polynom wurde bereitgestellt: \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\), das durch das Polynom geteilt werden muss \(\displaystyle s(x) = x+3\).

Beachten Sie, dass der Grad der Dividende \(\displaystyle deg(p) = 3\) ist, während der Grad des Divisors \(\displaystyle deg(s)) = 1\) ist.

Schritt 1: Der führende Begriff der Dividende \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) ist \(\displaystyle \frac{1}{3}x^3\), während der führende Begriff für den Divisor \(\displaystyle s(x) = x+3\) gleich \(\displaystyle x\) entspricht.

Der Begriff, den wir also mit \(x\) multiplizieren müssen, um zum führenden Begriff der Dividende zu gelangen, lautet \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\), also fügen wir diesen Begriff dem Quotienten hinzu.Außerdem multiplizieren wir dies mit dem Divisor, um \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\) zu erhalten, was wir an die Dividende subtrahieren müssen:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Schritt 2: In diesem Fall ist der führende Begriff des aktuellen Restes \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) \(\displaystyle -1x^2\) und wir wissen, dass der führende Begriff für den Divisor \(\displaystyle x\) ist.

Der Begriff, den wir also mit \(x\) multiplizieren müssen, um zum führenden Begriff des aktuellen Restes zu gelangen, lautet \(\displaystyle \frac{ -1x^2}{ x} = -x\), also fügen wir diesen Begriff dem Quotienten hinzu.Außerdem multiplizieren wir dies mit dem Divisor, um \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\) zu erhalten, was wir mit der aktuellen Erinnerung subtrahieren müssen:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Schritt 3: In diesem Fall ist der führende Begriff des aktuellen Restes \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) \(\displaystyle \frac{17}{4}x\) und wir wissen, dass der führende Begriff für den Divisor \(\displaystyle x\) ist.

Der Begriff, den wir also mit \(x\) multiplizieren müssen, um zum führenden Begriff des aktuellen Restes zu gelangen, lautet \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\), also fügen wir diesen Begriff dem Quotienten hinzu.Außerdem multiplizieren wir dies mit dem Divisor, um \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\) zu erhalten, was wir mit der aktuellen Erinnerung subtrahieren müssen:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

Dies schließt diese Berechnung ab, da der Grad des aktuellen Restes \(r(x) = -\frac{163}{12}\) geringer ist als der Grad des Divisors \(s(x) = x+3\).

Fazit: Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that