Polynomdiagramm

Verwenden Sie diesen Taschenrechner, wenn Sie Hilfe bei der Grafik einer Polynomfunktion benötigen.Der Prozess ist einfach: Sie müssen nur die Polynomfunktion eingeben, die Sie drapieren möchten.Sie können so etwas wie '3x^3 + x - 1' schreiben oder es mit dem Funktionsnamen wie 'p (x) = 3x^3 + x - 1' vornehmen.

Die Koeffizienten des bereitgestellten Polynoms müssen nicht unbedingt ganzzahlig sein, sie können Brüche oder gültigen algebraischen Expressionen sein.Das von Ihnen bereitgestellte Polynom kann vereinfacht werden oder nicht, es spielt keine Rolle.

Sobald das Polynom zur Verfügung gestellt wurde, können Sie optional die Bereiche von X -Werten bestimmen, die grafisch sind, und dann auf "Berechnen" klicken, und in Kürze werden alle Schritte des Prozesses angezeigt.

Polynomfunktionen sind eines der wichtigsten Objekte, die Sie in Algebra sowie in Kalkül finden.Außerdem führen Polynome zu der Notwendigkeit, Polynomgleichungen zu lösen, die überall in allen Bereichen des Lebens, auch über Mathematik, überall Anwendungen aufweisen.

Grundlagen der polynomfunktionen

Erinnern wir uns daran, dass eine Polynomfunktion die folgende Form hat:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

wo wir das annehmen, \(a_n \ne 0\) und wir sagen, dass das Polynomgrad In diesem Fall entspricht \(n\) und der führende Koeffizient ist \(a_n\).Die Laienmethode, um den Grad eines Polynoms zu definieren, besteht darin, dass es der höchsten Kraft entspricht, die in der Polynomexpression vorhanden ist.

Zum Beispiel ist \(p(x) = 3x^2 + 2x - 1\) ein Polynom von Grad 2, und sein führender Koeffizient beträgt 3. jetzt ist \(p(x) = \sin(3x^2 + 2x - 1)\) zum Beispiel kein Polynom.

Wie mache ich polynomegrafiken?

Grafing Polynome im Prinzip zeigen dasselbe wie die Grafik einer anderen Funktion.Wenn Sie es von Hand tun würden, würden Sie mehrere Werte für x und y tabellieren, und Sie würden eine Kurve verfolgen, die mehr oder weniger durch die Punkte gehen, die Sie in Ihrer Tabelle erhalten.

Natürlich ist diese Methode ein bisschen primitiv, da wir im Allgemeinen nicht unbedingt den vollständigen Graphen einer Funktion kennen, indem wir nur eine Reihe von Punkten kennen, die wir tabellieren.

Glücklicherweise ist die Aufgabe für Polynome etwas einfacher, und in Wirklichkeit können wir viel über das Diagramm wissen, indem wir ihren führenden Koeffizienten und seinen Abschluss kennen.

Schritte zum grafieren von polynomfunktionen

Die Grafik eines Polynoms hängt letztendlich vom spezifischen Koeffizienten jedes Polynoms ab.Aber wir können einige starke Aussagen über das Endverhalten eines Polynome und die Existenz realer Wurzeln machen.

Erinnern wir uns daran, dass das Endverhalten eines Polynoms das Verhalten des Polynoms ist, wenn x sehr groß und negativ ist und wenn X sehr groß und positiv ist.

• Schritt 1: Identifizieren Sie die Polynomfunktion und vereinfachen Sie, wenn Sie können, da es einfacher ist, die vereinfachten Ausdrücke zu gratschen
• Schritt 2: Kennen Sie die Wurzeln des Polynoms?Wenn dies echte Wurzeln sind, kennen Sie die Punkte, an denen das Polynom die X-Achse überschreitet, was Ihnen eine starke grafische Referenz ergibt
• Schritt 3: Wenn der Grad des Polynoms ungerade ist, ist das Endverhalten für große negative X -Werte und große positive X -Werte entgegengesetzt.Wenn der führende Koeffizient positiv ist, ist das Polynom für große negative X -Werte sehr groß und negativ, und für große positive X -Werte ist das Polynom sehr groß und positiv.Wenn der führende Koeffizient negativ ist, ist das Polynom für große negative X -Werte sehr groß und positiv, und für große positive X -Werte ist das Polynom sehr groß und negativ
• Schritt 4: Wenn der Grad des Polynoms ausgeglichen ist, ist das Endverhalten für große negative X -Werte und große positive X -Werte gleich.Wenn der führende Koeffizient positiv ist, ist das Polynom für große negative und positive X -Werte sehr groß und positiv.Wenn der führende Koeffizient negativ ist, ist das Polynom für große negative und positive X -Werte sehr groß und negativ
• Schritt 5: Wenn der Grad des Polynoms seltsam ist, kreuzt das Polynom mindestens einmal die x-Achse (so dass es mindestens eine echte Wurzel hat), während das Polynom für einen geraden Grad die X-Achse nicht unbedingt überschreitet
• Schritt 6: Ein Polynom des Grades n wird die x-Achse höchstens n-mal überschreiten.Zum Beispiel kann ein Polynom von 4 Grad 4 die x-Achse höchstens viermal überschreiten

Zum Beispiel kann ein kubisches Polynom die x-Achse höchstens dreimal überqueren, muss es aber nicht.

Grafikrechner

Was sind die Vorteile der Verwendung eines Grafikrechners?Viele.Das heißt nicht, dass es keine gute Fähigkeit ist, ein Polynom mit Stift und Papier genau zu skizzieren.

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

• Wirbel 1: Sie stellen sicher, dass Sie eine genaue Darstellung des tatsächlichen Diagramms des Polynoms erhalten
• Wirbel 2: Sie können es verwenden, um Ihre eigenen Arbeiten zu überprüfen, um sicherzustellen, ob Sie den richtigen Schritten verfolgen
• Wirbel 3: Ein guter Taschenrechner mit Wählen Sie ein geeignetes Fenster, um die relevantesten Aspekte des Diagramms anzuzeigen

Ein gutes Diagramm kann Ihnen viel über die Eigenschaften einer Funktion erzählen, und das gleiche gilt für ein Polynom.Diagramme Polynome können Ihnen dabei helfen, wirklich zu visualisieren, welche Art von Wurzeln das Polynom hat.

Tipps und tricks

Seien Sie vorsichtig, wenn Sie in einem Polynomdiagramm überlesen, was Sie sehen.Sie können nicht ohne weiteres über Wurzeln mit Multiplizität erzählen, daher ersetzt nichts die tatsächliche Funktion.

Wenn Sie andere Arten von Funktionen ausprobieren möchten, versuchen Sie dies Funksgrafik Werkzeug.

Beispiel: grafing polynomfunktionen

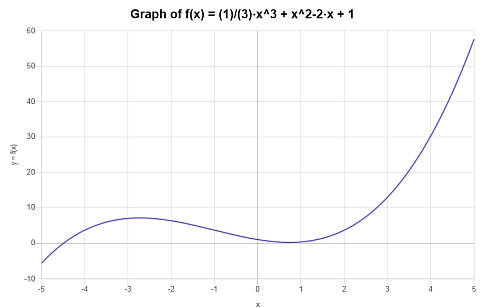
Graphen Sie das folgende Polynom: \(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)

Lösung: Wir erhalten den folgenden Polynomausdruck, den wir berechnen müssen: \(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\).

Der vorgesehene Ausdruck ist nicht reduzierbar, daher gibt es nichts zu vereinfachen.

Das folgende Diagramm wird für den gegebenen Polynomausdruck auf dem Intervall \([-5, 5]\) erhalten:

Beispiel: polynomdiagramm

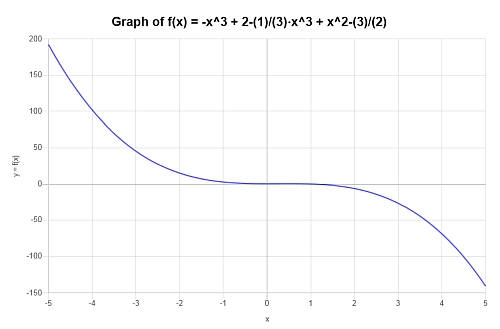
Vereinfachen und Diagramm: \(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)

Lösung: Jetzt müssen wir mit: \(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\) arbeiten.

Die folgende Vereinfachung wird erhalten:

Dies schließt den Prozess der polynomialen Vereinfachung ab.

Also wird das folgende Diagramm für \(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\) im Intervall \([-5, 5]\) erhalten:

Beispiel: mehr polynomgraphen

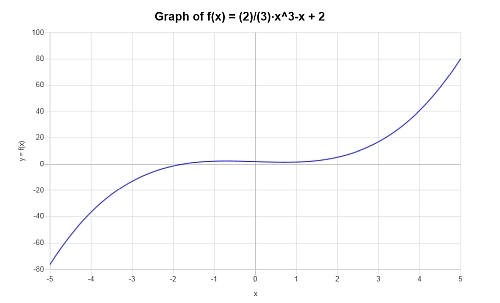
Finden Sie die Grafik des folgenden Polynoms \( p(x) = \frac{2}{3} x^3 - x +2 \).

Lösung: In diesem Beispiel ist das bereitgestellte Polynom: \(\displaystyle \frac{2}{3} x^3 - x +2 \).

In diesem Fall ist der vorgesehene Ausdruck nicht reduzierbar, daher gibt es nichts zu vereinfachen.

Das folgende Diagramm wird für den gegebenen Polynomausdruck auf dem Intervall \([-5, 5]\) erhalten:

Mehr polynomrechner

Das Diagramm von Polynomen ist äußerst nützlich, da es uns die Hauptmerkmale ihres Verhaltens um ihre Wurzeln und ihr Endverhalten zeigt.Das Diagramm geht normalerweise Hand in Hand mit der Identifizierung von ungefähr dort, wo Wurzeln sein könnten, was mit verwenden könnte Polynom Faktoring auch.

Obwohl wir viel über das Polynom wissen, nur wenn wir es drapieren, müssen wir immer noch den Prozess des Versuchs durchlaufen Funde Sies Begründung Wurzeln wie der Ausgangspunkt für Polynomgleichungen lösen mit Grad höher als 2 (dies ist das nicht quadratische Gleisungen ).

Systematisch rationale Wurzeln erraten oder finden, gepaart mit der Verwendung Lange Division oder Synthetische Abteilung Also, um die zu benutzen Faktorsatz kann zu einer erfolgreichen Suche nach führen Polynomwurzeln Aber ein solcher Ansatz funktioniert nicht immer, und oft müssen Sie sich auf den Taschenrechner verlassen, um numerische Näherungen zu finden.