Weitere informationen zum normalwahrscheinlichkeitsdiagramm

Ein Normalwahrscheinlichkeitsdiagramm ist ein Diagramm, das typischerweise verwendet wird, um die Normalität der Verteilung zu beurteilen, zu der die übergebenen Stichprobendaten gehören.

Es gibt verschiedene Arten von Normalitätsdiagrammen (PP, QQ und andere), aber sie basieren alle auf derselben Idee. Die theoretischen Quantile einer Standardnormalverteilung werden den beobachteten Quantilen gegenübergestellt.

Wenn die Beispieldaten also aus einer normalverteilte Population , dann sollte das Normalwahrscheinlichkeitsdiagramm wie ein 45 aussehen ^o Linie mit zufälligen Abweichungen. Wenn dies nicht der Fall ist und das Muster des Normalwahrscheinlichkeitsdiagramms signifikant/systematisch vom Normalwahrscheinlichkeitsdiagramm abweicht, sollte man vermuten, dass die Verteilung nicht normal ist.

Wie berechnet man ein normalwahrscheinlichkeitsdiagramm?

Es gibt mehrere konkrete Schritte, die Sie in einer bestimmten Reihenfolge ausführen müssen, um ein normales Wahrscheinlichkeitsdiagramm zu erstellen

1. In diesem konkreten Fall werden die Daten in aufsteigender Reihenfolge sortiert und wir nennen diese Daten \(X_1, X_2, ...., X_i , ...., X_n\).
2. Für jedes \(X_i\) in dieser Folge geordneter Daten berechnen wir die theoretischen Häufigkeiten \(f_i\), die mit der folgenden Formel angenähert werden:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. Wir berechnen dann auch \(z_i\), den entsprechenden zugehörigen Z-Score als
\[ z_i = \Phi^{-1}(f_i)\]
4. Anschließend wird das Normalwahrscheinlichkeitsdiagramm erstellt, indem die geordneten X-Werte (Ihre Beispieldaten) auf der horizontalen Achse und die entsprechenden \(z_i\)-Werte auf Ihrer vertikalen Achse aufgetragen werden.

Normalwahrscheinlichkeitsdiagramm excel

Sie können ein normales Wahrscheinlichkeitsdiagramm in Excel zeichnen, aber es dauert einige Zeit. Yo

Rechner für die normalverteilung und mehr

Andere Diagrammersteller, die Sie verwenden können, sind unsere Normalverteilungsgraph , Verklemmungshersteller streuen oder unsere Pareto-Charthersteller. .

Beispiel: berechnung eines normalwahrscheinlichkeitsdiagramms

Frage : Ihnen stehen die folgenden Beispieldaten zur Verfügung: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 und 23. Erstellen Sie ein Normalwahrscheinlichkeitsdiagramm.

Lösung:

Wir müssen ein Normalwahrscheinlichkeitsdiagramm erstellen. Dies sind die bereitgestellten Beispieldaten:

Beobachtung:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

Es müssen die theoretischen Häufigkeiten \(f_i\) sowie die zugehörigen Z-Scores \(z_i\) für \(i = 1, 2, ..., 33\) berechnet werden:

Beachten Sie, dass die theoretischen Frequenzen \(f_i\) mithilfe der folgenden Formel angenähert werden:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

Dabei entspricht \(i\) der Position im geordneten Datensatz und \(z_i\) dem zugehörigen Z-Score. Die Berechnung erfolgt wie folgt:

\[ z_i = \Phi^{-1}(f_i)\]

Man erhält folgende Tabelle

Position (i)	X (Aufsteigende Reihenfolge)	F ich	z ich
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

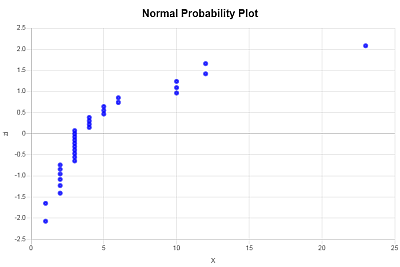
Das Normalverteilungsdiagramm wird erstellt, indem die X-Werte (Ihre Stichprobendaten) auf der horizontalen Achse und die entsprechenden \(z_i\)-Werte auf der vertikalen Achse aufgetragen werden. Das folgende Normalverteilungsdiagramm ergibt sich: