Mehr über dieses tool zur berechnung der wahrscheinlichkeit der normalverteilung für stichprobenverteilungen

Wenn eine Folge von normalverteilten Variablen \(X_1, X_2, ...., X_n\) gemittelt wird, erhält man den Stichprobenmittelwert

\[\bar X = \frac{1}{n}\sum_{i=1}^n X_i\]

Da jede Linearkombination von Normalvariablen ebenfalls normalverteilt ist, ist auch der Stichprobenmittelwert \(\bar X\) normalverteilt (unter der Annahme, dass jedes \(X_i\) normalverteilt ist). Die Verteilung von \(\bar X\) wird im Allgemeinen als die Stichprobenverteilung der Mittelwerte der Stichprobe .

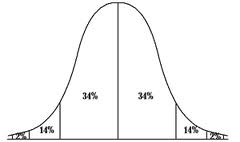
Eine andere Bezeichnung für die Normalverteilung ist die Gaußverteilung oder die glockenförmige Verteilung.

Wie berechnet man die stichprobenverteilung?

Angenommen, dass \(X_i \sim N(\mu, \sigma^2)\) für alle \(i = 1, 2, 3, ...n\) normalverteilt ist, dann ist \(\bar X\) normalverteilt mit demselben gemeinsamen Mittelwert \(\mu\), aber mit einer Varianz von \(\displaystyle\frac{\sigma^2}{n}\).

Daraus ergibt sich, dass \(\bar X\) auch bei \(\mu \) zentriert ist, aber seine Streuung ist geringer als die für jedes einzelne \( X_i \). Je größer der Stichprobenumfang ist, desto geringer ist die Streuung von \(\bar X\).

Die formel der normalverteilung

Die Formel für die Normalverteilung ist eine relativ schwierige Formel, die Sie nicht manuell bearbeiten werden. Die Formel lautet:

\[ f(x)=\frac{1}{\sigma {\sqrt {2\pi }}} e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}\]

Die formel für die stichproben-normalverteilung

Der Schlüssel bei der Arbeit mit Stichprobenverteilungen ist die Tatsache, dass, wenn \(\mu\) der Mittelwert der Grundgesamtheit und \(\sigma\) die Standardabweichung der Grundgesamtheit ist, dann

\[ \displaystyle \frac{\bar X - \mu}{\sigma}\]

hat eine Standardnormalverteilung. Dies ist von entscheidender Bedeutung, denn damit können wir alle Stichprobenverteilungen reduzieren auf standard-Normalwahrscheinlichkeitsberechnungen .

Vereinfacht ausgedrückt, reduzieren Sie die Berechnung einer beliebigen Normalverteilungswahrscheinlichkeit auf die berechnung von z-Scores .

Durch die Reduzierung aller Normalverteilungsberechnungen auf die Arbeit mit z-Werten benötigen Sie nur eine Standard-Normaltabelle, in der Sie die z-Werte finden, oder ein Tool wie diesen Rechner oder Excel.

Was ist der mittelwert der stichprobenverteilung

Der Mittelwert von Stichprobenverteilungen, \(\mu(\bar X)\), ist derselbe wie der zugrunde liegende Mittelwert der Verteilung \(\mu\).

Standardabweichung der stichprobenverteilung

Im Gegensatz zum Mittelwert kann die Standardabweichung der Stichprobenmittelwerte anhand der Formel berechnet werden:

\[s(\bar X) = \displaystyle \frac{\sigma}{\sqrt n}\]

Rechner im zusammenhang mit der normalverteilung

Wenn Sie normale Wahrscheinlichkeiten für eine einzelne Beobachtung \(X\) berechnen wollen, können Sie diesen Rechner mit \(n=1\) verwenden, oder Sie können unseren regulären Normalverteilungsrechner .

Oft ist man an dem umgekehrten Prozess interessiert: Bei einer gegebenen Wahrscheinlichkeit möchte man die Punktzahl finden, bei der die Wahrscheinlichkeit rechts von dieser Punktzahl die gegebene Wahrscheinlichkeit ist, wofür man eine invnorm-Rechner

Wenn Sie eine grafische Visualisierung benötigen, können Sie auch direkt unsere ersteller von Normalverteilungsgraphen .

Um zu beurteilen, ob eine Stichprobe tatsächlich einer Normalverteilung entstammt, können Sie auch eine normalwahrscheinlichkeitsdarstellung und sehen Sie sich das erhaltene Muster an. Wenn es ziemlich linear aussieht, deutet dies darauf hin, dass die Stichprobe wahrscheinlich aus einer normalverteilten Propulation stammt.

Beispiel:

Frages : Betrachten wir eine Normalverteilung, bei der der Mittelwert der Grundgesamtheit 12 und die Standardabweichung der Grundgesamtheit 3,4 beträgt. Angenommen, Sie nehmen Stichproben mit dem Umfang n = 16. Wie hoch ist die Wahrscheinlichkeit, dass die Stichprobenmittelwerte im Intervall (11,3, 12,4) liegen?

Lösung:

Im Folgenden werden der Populationsmittelwert \((\mu)\), die Populationsstandardabweichung \((\sigma)\) und der Stichprobenumfang \((n)\) angegeben:

Population Mean \((\mu)\) =	\(12\)
Population Standard Deviation \((\sigma)\) =	\(3.4\)
Sample Size \((n)\) =	\(16\)
Event to compute its probability =	\(11.3 \leq \bar X \leq 12.4\)

Wir müssen \(\Pr(11.3 \leq \bar X \leq 12.4)\) berechnen. Die entsprechenden zu berechnenden z-Werte sind:

\[Z_{lower} = \frac{X_1 - \mu}{\sigma/\sqrt{n}} = \frac{ 11.3 - 12}{ 3.4/\sqrt{16}} = -0.82 \] \[Z_{upper} = \frac{X_2 - \mu}{\sigma/\sqrt{n}} = \frac{ 12.4 - 12}{ 3.4/\sqrt{16}}= 0.47 \]

Unter Verwendung der Eigenschaften der Normalverteilung, wenn \(X ~ N(\mu, \sigma)\), dann haben die Variablen \(Z_{lower} = \displaystyle \frac{X_1 - \mu}{\sigma/\sqrt{n}} \) und \(Z_{upper} = \displaystyle \frac{X_2 - \mu}{\sigma/\sqrt{n}} \) eine Standardnormalverteilung. Daher wird die Wahrscheinlichkeit wie folgt berechnet:

\[ \begin{array}{ccl} \Pr(11.3 \leq \bar X \leq 12.4) & = & \Pr\left(\displaystyle \frac{ 11.3 - 12}{ 3.4 / \sqrt{ 16}} \leq \frac{ \bar X - 12}{ 3.4 / \sqrt{ 16}} \leq \frac{ 12.4 - 12}{ 3.4 / \sqrt{ 16}}\right) \\\\ \\\\ & = & \displaystyle\Pr\left(\frac{ 11.3 - 12}{ 3.4 / \sqrt{ 16}} \leq Z \leq \frac{ 12.4 - 12}{ 3.4 / \sqrt{ 16}}\right) \\\\ \\\\ & = & \displaystyle \Pr\left(-0.82 \leq Z \leq 0.47\right) \\\\ \\\\ & = & \displaystyle \Pr\left(Z \leq 0.47\right) - \Pr\left(Z \leq -0.82\right) \\\\ \\\\ & = & 0.681 - 0.2051 \\\\ \\\\ & = & 0.4759 \end{array}\]

Auf der Grundlage der vorgelegten Informationen wird daher der Schluss gezogen, dass \( \Pr(11.3 \leq \bar X \leq 12.4) = 0.4759\).