So verwenden sie den rechner für kritische t-werte

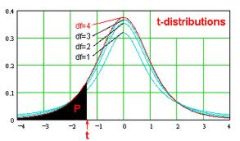
Mehr Informationen über Kritische Werte für die t-Verteilung : Zunächst einmal sind kritische Werte Punkte an den Schwänzen einer bestimmten Verteilung, mit der Eigenschaft, dass die Fläche unter der Kurve für diese kritischen Punkte in den Schwänzen gleich dem gegebenen Wert von \(\alpha\) ist

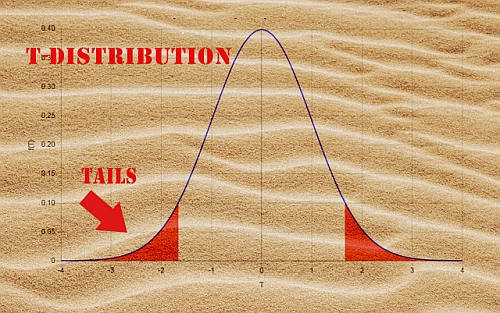
Die Verteilung ist in diesem Fall die T-Student-Verteilung. Allgemein ausgedrückt entsprechen die kritischen Werte für einen zweiseitigen Fall zwei Punkten links und rechts vom Zentrum der Verteilung, die die Eigenschaft haben, dass die Summe der Fläche unter der Kurve für den linken Schwanz (ab dem linken kritischen Punkt) und der Fläche unter der Kurve für den rechten Schwanz gleich dem gegebenen Signifikanzniveau \(\alpha\) ist.

Kritische t-werte

Im Falle eines Linksschwanzes entspricht der kritische Wert dem Punkt links vom Zentrum der Verteilung, mit der Eigenschaft, dass die Fläche unter der Kurve für den linken Schwanz (vom kritischen Punkt nach links) gleich dem angegebenen Signifikanzniveau \(\alpha\) ist.

Im Falle eines Rechtsschwanzes entspricht der kritische Wert dem Punkt rechts vom Zentrum der Verteilung, mit der Eigenschaft, dass die Fläche unter der Kurve für den rechten Schwanz (vom kritischen Punkt nach rechts) gleich dem angegebenen Signifikanzniveau \(\alpha\) ist.

Was sind die wichtigsten eigenschaften der t-verteilung?

Die wichtigsten Eigenschaften der T-Verteilung und ihrer kritischen Punkte sind:

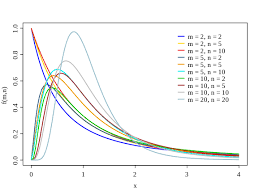
• Die t-Verteilung ist eine symmetrische, kontinuierliche Verteilung, die durch die Anzahl der Freiheitsgrade (df) bestimmt wird


• Die t-Verteilung konvergiert (im verteilungstechnischen Sinne) zur Standardnormalverteilung (Z-Verteilung), wenn die Freiheitsgrade (df) gegen unendlich konvergieren


• Die t-Verteilung wird für verschiedene t-Tests verwendet, bei denen die Standardabweichung der Grundgesamtheit nicht bekannt ist


• Da die t-Verteilung symmetrisch ist, sind die kritischen Punkte für den zweiseitigen Fall symmetrisch in Bezug auf den Mittelpunkt der Verteilung


• Da die t-Verteilung symmetrisch ist, ist die Ermittlung der kritischen Werte für einen zweiseitigen Test mit einer Signifikanz von \(\alpha\) identisch mit der Ermittlung einseitiger kritischer Werte für eine Signifikanz von \(\alpha\)/2

Die t-Verteilung ist die zugrunde liegende Verteilung für die in statistischen Anwendungen sehr häufig verwendete T-Test für die Gepaarte-Probe und T-Test für Zwei Unabhängige Probe . Diese Tests sind entscheidend für die Bewertung der statistischen Signifikanz der Unterschiede bei gepaarten und nicht gepaarten Daten.

Brauche ich eine t-kritische wertetabelle?

Technisch gesehen können Sie eine t-Kritikwerttabelle verwenden, die Sie hinten in Ihrem Statistikbuch 101 finden, aber mit dieser rechner für kritische t-Werte wird diese Notwendigkeit beseitigen. Wenn Sie mit statistischen Tabellen arbeiten, müssen Sie die richtige Tabelle und Position für die entsprechende Anzahl von Freiheitsgraden und Alpha-Niveau finden.

Bei unserem Rechner geben Sie die Freiheitsgrade und das Alphaniveau an und drücken einen Knopf. Dann erhalten Sie den gewünschten t-kritischen Wert sowie die t-Verteilungsdiagramm mit dem/den korrekten Schweif(en), der/die mit dem/den kritischen Wert(en) verbunden ist/sind.

Beispiel: Beispiel für die berechnung des kritischen t-wertes

Wie hoch ist der t-kritische Wert für Alpha = 0,01 bei einem zweiseitigen Test und einem Stichprobenumfang von n = 31?

Lösung: Erstens: Die Anzahl der Freiheitsgrade ist df = n - 1 = 31 - 1 = 30. Für einen zweiseitigen Test müssen wir also den Wert der t-Verteilung mit 30 Freiheitsgraden finden, der eine Wahrscheinlichkeit von 0,01/2 = 0,005 am rechten Ende hat.

Daher ist der kritische t-Wert \(t_c = 2.750\). Da es sich um einen zweiseitigen Test handelt, sind die kritischen Werte \(t_c = \pm 2.750\).

Grafisch:

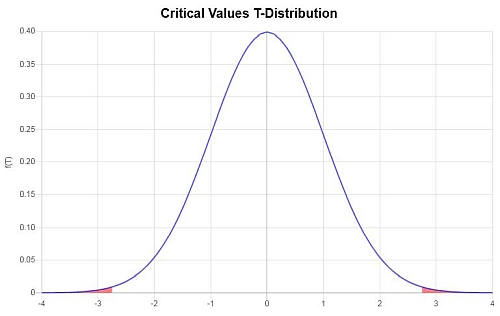
Außerdem ist die zugehörige Ablehnungsregion \(R = \{t: |t| > 2.750\}\)

Andere kritischer-wert-rechner

Dieser Rechner dient der Ermittlung von t-Werten. Wir haben viele andere Rechner für kritische Werte, wie zum Beispiel den rechner für z-kritische Werte , F-kritische Werte-Rechner , und die Chi-Quadrat-Rechner für kritische Werte .

Die Verwendung von kritischen Werten ist eine der gängigsten Methoden zur Prüfung statistischer Hypothesen, indem die Werte, die durch eine testwert-Rechner mit den entsprechenden kritischen Werten, da die kritischen Werte direkt zur Konstruktion von Ablehnungsbereichen verwendet werden.