Das Konzept der Funktion ist äußerst wichtig und in der Mathematik absolut allgegenwärtig. Aus diesem Grund müssen wir es gründlich auffrischen, bevor wir versuchen, einige der Vorteile zu verstehen, die sich später ergeben, wenn wir uns eingehender mit Kalkül-Themen wie Differenzierung und Integration befassen.

WAS IST EIN SET?

Das erste Element, das wir verstehen müssen, ist das Konzept von a einstellen . Ein Set ist einfach eine Sammlung von Elementen. Eine Menge wird also ganz einfach definiert, indem man weiß, welche Elemente zur Menge gehören und welche nicht. Es scheint eine supereinfache Aufgabe zu sein, und die Mengenlehre sollte einfach auf eindeutige Regeln zur Bestimmung der zu einer Menge gehörenden Elemente reduziert werden.

Definieren wir zum Beispiel die Menge der geraden Zahlen und nennen sie \(E\). Warum ist es überhaupt ein Set? Weil es eine eindeutige Regel gibt, um zu bestimmen, welche Elemente zu \(E\) gehören: Eine reelle Zahl \(x\) gehört zu \(E\), wenn sie durch 2 teilbar ist. Die Regel funktioniert eindeutig für jede einzelne reelle Zahl, die bestimmt, ob sie zu \(E\) gehört oder nicht. Warum ich "eindeutig" sage und immer wieder wiederhole. Weil es wichtig ist. Eindeutig bedeutet dies, dass es keine Möglichkeit gibt zu schließen, dass ein gegebenes \(x\) sowohl zu \(E\) gehört als auch nicht zu \(E\) gehört. Leider gehen die Dinge manchmal über unsere Vorstellungskraft hinaus. Entgegen unserer Intuition kann eine mit einer einfachen Zugehörigkeitsregel definierbare Menge zu einer mehrdeutigen (widersprüchlichen) Zugehörigkeitsklassifikation führen, wie Bertrand Russell in seinem berühmten Paradoxon zeigt. Russell hat gezeigt, dass eine genauere Definition des Satzes verwendet werden sollte.

Für alle praktischen Zwecke werden wir eine Menge als eine Sammlung von Elementen betrachten, die durch eine Zugehörigkeitsregel definiert werden können .

WAS IST DAS PRODUKT VON ZWEI SETS?

Es seien \(A\) und \(B\) Mengen im Kontext der oben angegebenen Definition. Das Produkt \(A\times B\) aus zwei Sätzen ist ein weiterer Satz, der als Satz aller möglichen geordneten Paare der Form \(\left( a, b \right)\) definiert ist, wobei \(a\) zu \(A\) und \(b\) zu \(B\) gehört. Dann ist \(A\times B\) eine Menge, und ihre Elemente sind geordnete Paare der Form \(\left( a ,b \right)\). Lassen Sie sich von dieser Notation nicht beeindrucken. Wenn ich "geordnete Paare der Form \(\left( a, b \right)\)" sage, ist das Symbol \(\left( a, b \right)\) ein zusammengesetztes Symbol, um ein Element anzuzeigen, das aus zwei Entitäten \(a\) und \(b\) besteht, und das erste Element als \(a\) und das zweite Element als \(b\) zu identifizieren . Das ist es. Anstelle von \(\left( a,b \right)\) hätten wir auch das Symbol \(a\_b\) wählen können, und es hätte in Ordnung funktioniert.

Sie müssen mir vergeben, aber ich muss die mathematische Definition des Produkts zweier Mengen schreiben (wir können auch Mengen multiplizieren ... was haben Sie gedacht, wir würden nur mit Zahlen aufhören, oder?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

Der Grund, warum ich die Definition schreibe, ist, dass Sie sie betrachten und erkennen, wie wir mit einer sehr kompakten Notation genau das sagen, wie ich sie im obigen Absatz mit Wörtern definiert habe. Ich hoffe, Sie werden die Angst vor dem Lesen von mathematischen Aussagen lockern. Mathematiker können manchmal flippige Leute sein, aber sie finden gute, eindeutige und kompakte Notationen. Folglich ist die mathematische Sprache SUPER leicht zu lesen. Recht? Recht? Bitte sag mir, dass ich Recht habe ...

Eine Randnotiz wird aus historischen Gründen das Produkt zweier Sätze \(A\times B\) normalerweise als a bezeichnet kartesisches Produkt .

JETZT DIE DEFINITION EINER FUNKTION (ENDLICH)

Ok, ich habe gelogen, es gibt noch einen Schritt, bevor ich definiere, was eine Funktion ist. Wir müssen das Konzept von definieren Beziehung . Was ist eine Beziehung? Über die übliche Verwendung als englisches Wort hinaus ist eine Beziehung einfach eine Teilmenge eines kartesischen Produkts. JEDE Teilmenge eines kartesischen Produkts ist eine Beziehung. Wenn also \(A\) und \(B\) Mengen sind, ist eine Menge \(R\) eine Beziehung, wenn \(R\subseteq A\times B\). Da jede Menge als Teilmenge ihrer selbst betrachtet werden kann, sind alle kartesischen Produkte selbst Beziehungen.

Setzen Sie es auf einen Rahmen:

Eine Beziehung ist eine Menge, die eine Teilmenge eines kartesischen Produkts ist

Lassen Sie uns grafischer werden. Betrachten Sie die Menge \(A=\left[ 0,1 \right]\) (dies sind alle reellen Zahlen, die größer oder gleich 0 sind und auch kleiner oder gleich 1 sind). Was ist das kartesische Produkt \(A\times A\)? Lassen Sie uns nachahmen, was wir gerade gelernt haben. Das kartesische Produkt \(A\times A\) ist \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). In diesem Fall handelt es sich um die Menge aller Paare\(\left( x, y \right)\), wobei sowohl \(x\) als auch \(y\) zu \(\left[ 0,1 \right]\) gehören. Kartesische Produkte sind normalerweise leicht grafisch darzustellen. Schauen Sie sich den schattierten Bereich unten an:

Was würde nun eine Beziehung herstellen? Wir können alles, was wir wollen, aus dem schattierten Bereich oben herausarbeiten, und was übrig bleibt, ist eine Beziehung in \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Zum Beispiel können wir die "Ecken" ausschneiden, um die folgende Unterregion zu erhalten:

Die obige Region (Menge) ist eine Beziehung. Warum? Weil es eine Teilmenge des kartesischen Produkts \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) ist. Aber wir können noch mehr herausarbeiten. Wie wäre es mit einem Viertelkreis? Siehe die Region unten.

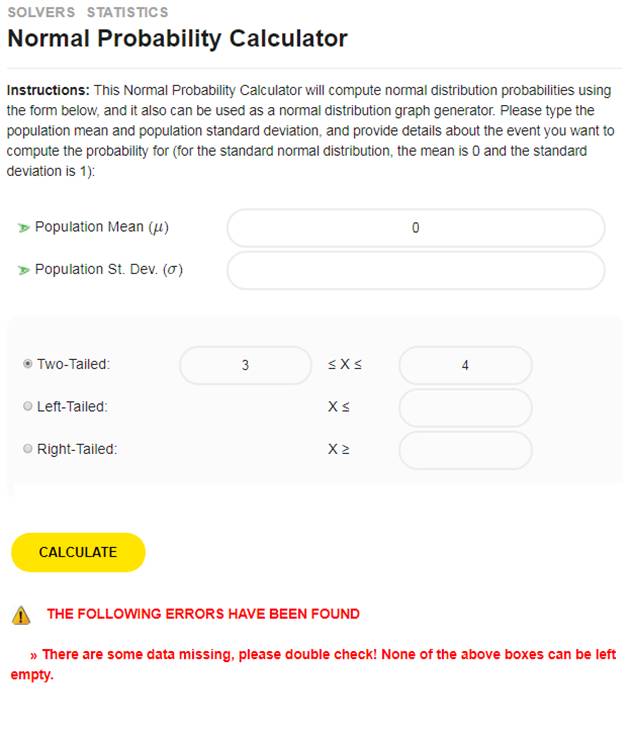
Die obige Region (Menge) ist eine Beziehung. Warum? Auch hier handelt es sich um eine Teilmenge des kartesischen Produkts \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

Lassen Sie mich nun ein Beispiel für zwei Beziehungen in \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) geben. Siehe die folgenden Grafiken:

Beziehung 1

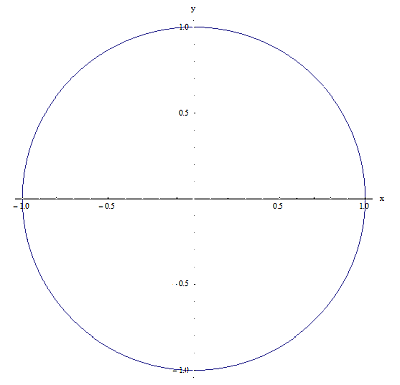
Beziehung 2

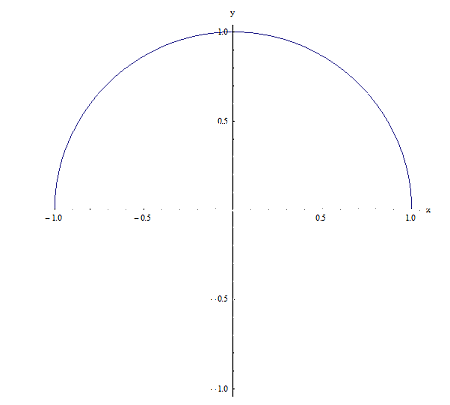
Sie sind beide offensichtlich Beziehungen (weil sie beide im kartesischen Produkt \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) enthalten sind, aber sie haben einen wesentlichen Unterschied: Für Beziehung 1 gibt es für einen gegebenen Punkt x auf \(\left[ -1,1 \right]\) zwei Punkte \({{y}_{1}}\) und \({{y}_{2}}\), die die Eigenschaft haben, dass \(\left( x,{{y}_{1}} \right)\) und \(\left( x,{{y}_{2}} \right)\) gehören zu Beziehung 1. Zum Beispiel gibt es für x = 0 zwei Punkte \({{y}_{1}}=1\) und \({{y}_{2}}=-1\), so dass \(\left( 0,1 \right)\) und\(\left( 0,-1 \right)\) zu Beziehung 1 gehören. Nun, für Beziehung 2 ist dies nicht der Fall, weil zum Beispiel für x = 0 nur \(y=1\) das ist macht den Punkt \(\left( 0,1 \right)\) zu Beziehung 1 gehören.

Schließlich können wir eine Funktion definieren: Eine Funktion \(R\) ist eine Menge, die eine Beziehung ist, und sie hat auch die Eigenschaft, dass, wenn der Punkt \(\left( x,y \right)\) zu \(R\) gehört, es keinen anderen Punkt \(\bar{y}\) gibt, der sich von \(y\) unterscheidet, der die Eigenschaft hat, dass \(\left( x,\bar{y} \right)\) zu \(R\) gehört auch. Mit anderen Worten, eine Funktion ist eine Beziehung zu der zusätzlichen Anforderung, dass jedes \(x\) in seiner Domäne nur einem \(y\) zugeordnet ist.

Woher weiß man, wie man zwischen einer Funktion und einer Beziehung unterscheidet?

Gadgets! Wir verwenden einen kleinen Trick, den „Test der vertikalen Linie“: Wir zeichnen eine imaginäre vertikale Linie und bewegen sie von links nach rechts und erstellen eine mentale Karte, wo die vertikale Linie die Beziehung schneidet.

• Wenn an JEDEM Punkt die vertikale Linie die Beziehung an MEHR als einem Punkt schneidet, besteht die Beziehung den Test der vertikalen Linie nicht und die Beziehung ist keine Funktion

• Wenn an JEDEM Punkt die vertikale Linie die Beziehung nirgendwo an MEHR als einem Punkt schneidet, besteht die Beziehung den vertikalen Linientest und die Beziehung ist eine Funktion

Siehe die beiden folgenden Beispiele:

Beispiel 1: Der vertikale Linientest besteht nicht, da die in der Abbildung gezeigte vertikale Linie die Beziehung an mehr als einem Punkt schneidet: KEINE FUNKTION

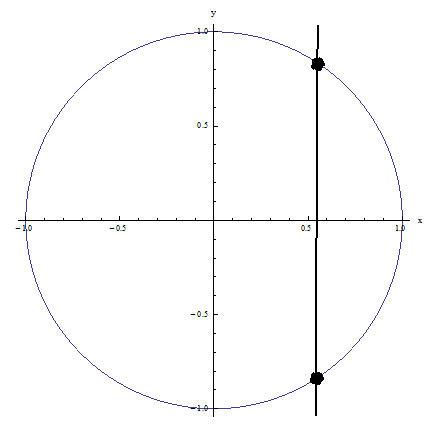
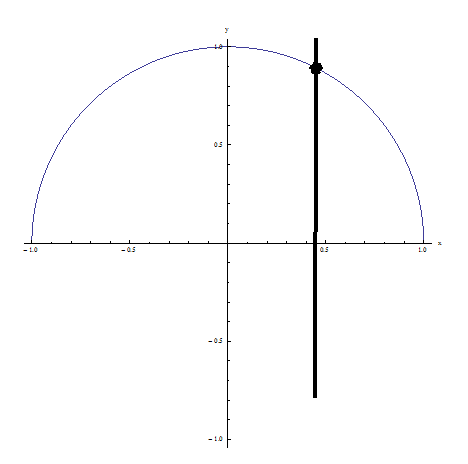
Beispiel 2: Es besteht den vertikalen Linientest, da keine vertikale Linie die Beziehung an mehr als einem Punkt schneidet: ES IST EINE FUNKTION!

Es gibt viele grafische Anwendungen, die mit Funktionen ausgeführt werden können, einschließlich der Berechnung von horizontalale Asymptoten , vertikale Asymptoten und gegebenenfalls schräge Asymptoten.