Polynomfunktionen

Dies Polynomfungion -Wiederaufnahme Hilft Ihnen dabei, Polynomefunktionen zu berechnen, indem Sie jeden von Ihnen bereitgestellten Polynomausdruck berechnen und vereinfachen.

Sie können jede Art von Expression mit Polynomen bereitstellen, und die Berechnung wird durchgeführt und die erforderlichen Vereinfachungsschritte werden ausgeführt, um eine Polynomfunktion in ihrer kompaktesten Form zu hinterlassen.Dann wird ein Polynomdiagramm bereitgestellt

Sobald ein gültiger Polynomausdruck bereitgestellt wurde, können Sie auf die Schaltfläche unten klicken, die Schaltfläche "Berechnen" und alle erforderlichen Schritte des Prozesses werden angezeigt.

Die Fraktionenalgebra beinhaltet Fraktionsumwandlung wie die Verwendung des gemeinsamen Nenners und die Verwendung grundlegender arithmetischer Regeln.Alles in allem kann der Prozess der Berechnung mühsam sein, obwohl er systematisch ohne viel Problem erfolgen kann.

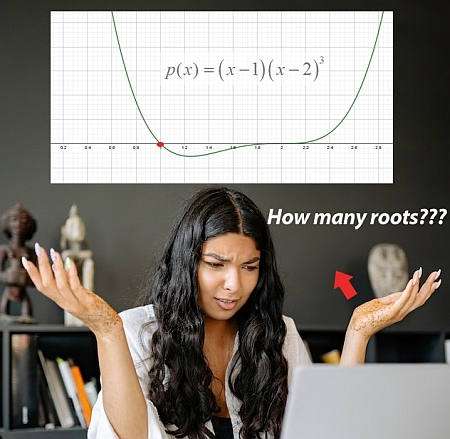
Was ist eine polynomfunktion?

Polynome sind in der einfachsten Erklärung die Funktionen, die nur aus Kräften von \(x\) bestehen, möglicherweise multipliziert mit numerischen Konstanten, die hinzugefügt (oder subtrahiert) Togheter.Zum Beispiel ist \(p(x) = x^3 + 2x^2 + 1\) eine Polynomfunktion, da sie aus den Kräften von \(x\) multipliziert mit Konstanten besteht, addiert.In diesem Fall ist \(1 = x^0\) eine Konstante auch eine Kraft von \(x\).:

Im Allgemeinen hat eine Polynomfunktion die folgende Form:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

mit \(a_n \ne 0\).In diesem Fall sagen wir, dass die Polynomgrad (oder seine Reihenfolge) ist \(n\), was die höchste Leistung in der Polynomfunktion ist.

Außerdem wird der Koeffizient \(a_n\) genannt Leitkoeffizient und \(a_n x^n\) wird das genannt Führer Begriff .Der führende Koeffizient und der Grad eines Polynoms bestimmen sein Endverhalten (dies ist das Verhalten, wenn der absolute Wert von x groß ist).

Was sind die schritte für die arbeit mit einer polynomfunktion?

• Schritt 1: Identifizieren Sie deutlich den Ausdruck, mit dem Sie arbeiten möchten, erweitern und vereinfachen
• Schritt 2: Überprüfen Sie, ob die Begriffe, die die Variable X betreffen
• Schritt 3: Stellen Sie sicher, dass alle Kräfte von X mit Konstanten multipliziert werden (was "1" sein könnte), und diese Begriffe erscheinen als hinzugefügt oder im Ausdruck subtrahiert

Es ist wichtig sicherzustellen Faktorsatz , das Restsatz und der Rational Zero Theorem , Die Ößsternst Nutzlich Sind, um Die Lösungen für Polynomgichungen Zu Funde, stirb in Verschiedungen Weitgehend Verendet Werden.

Auch der Vorteil des Umgangs mit Polynomfunktionen besteht darin, dass Sie leicht durchführen können Aufteilung von Polynomen entweder durch Verwendung Lange Division , oder Synthetische Abteilung Falls der Divisor linear ist.

Gibt es wichtige polynomfunktionen?

In der Tat.Es gibt die berüchtigten Polynome von Grad 2, die wir nennen Quadratische Polynom , die ausführlich in Basisalgebra untersucht werden.Der Grund dafür ist, dass sie mit präzisen Formeln vollständig analysiert werden können.Zum Beispiel haben Sie eine Formel für Den Scheieitelpunkt und die berühmte quadratische Formel wird verwendet, um Wurzeln für zu finden Quadratische Polynom :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Es gibt auch die Polynome von Grad 2, die wir nennen Kubische Polynom , die auch explizite Formeln haben, die jedoch normalerweise als komplexer angesehen werden und in der Regel nicht in grundlegenden Algebra -Kursen bedeckt sind.

Was weiß ich über das endverhalten eines polynoms?

Das Endverhalten eines Polynoms hängt letztendlich vom Polynom selbst ab, aber einige Dinge können aufgrund ihres Abschlusses gesagt werden

• Tatsache 1: Für quadratische Polynome öffnet sich das Diagramm nach oben (wenn der führende Koeffizient positiv ist) oder nach unten (wenn der führende Koeffizient negativ ist) und die Funktion konvergiert auf beiden Seiten zu unendlich oder abzüglich Unendlichkeit (abhängig vom Vorzeichen des führenden Koeffizienten)
• Tatsache 2: Für Polynome mit Grad, der seltsam ist (z. B. mit Grad 3), hat mindestens eine reale Wurzel, und die Funktion konvergiert auf der einen Seite auf unendlich und auf der anderen Seite abzüglich Unendlichkeit
• Fakt 3: Für Polynome mit Grad, der gleichmäßig ist (zum Beispiel mit Grad 4) gibt es keine unbedingt echten Wurzeln (ein Punkt, den er in der x-Achse überschreitet), und die Funktion konvergiert zu unendlich oder abzüglich Unendlichkeit (je nachdemdas Zeichen des führenden Koeffizienten) auf beiden Seiten

Polynome laufen also für große Werte von x groß, und ob ihre Werte positiv oder negativ für X (im Endverhalten) sind, hängt vom Vorzeichen des führenden Koeffizienten ab.

Tipps: was sind die vorteile der verwendung eines polynomfunktionsrechners

Polynomkalzulatoren können sicherstellen, dass Sie zur richtigen Antwort ankommen.In der Tat, Polynomberechnungen sind nicht kompliziert, aber sie können umständlich sein und es ist nicht schwer, Fehler zu machen.

Vermeiden Sie algebraische Fehler, indem Sie sicherstellen, dass Sie Ihre Arbeit mit diesem Taschenrechner überprüfen, damit Sie die Konsistenz der endgültigen Antwort und die Schritte zur Erreichung dorthin sicherstellen können.

Beispiel: polynomfunktion

Berechnen Sie die folgende Polynomfunktion \((x-3)(x-1)(x-4)\)

Lösung: Wir erhalten den folgenden Polynomausdruck, den wir berechnen müssen: \(\displaystyle (x-3)(x-1)(x-4)\).

Die folgende Berechnung wird erhalten:

Dies schließt den Prozess der polynomialen Vereinfachung ab.

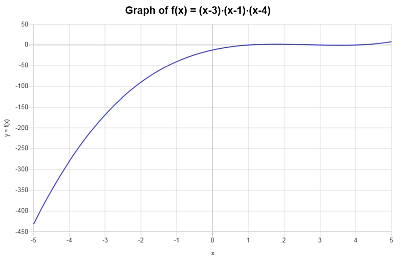
Das folgende Diagramm wird für \(\displaystyle x^3-8x^2+19x-12\) im Intervall \([-5, 5]\) erhalten:

Beispiel: polynomfunktionsberechnung

Ist dies eine Polynomfunktion: \(\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)

Lösung:

Wir erhalten den folgenden Polynomausdruck, den wir berechnen müssen: \(\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\).

Die folgende Berechnung wird erhalten:

was den Vereinfachungsprozess beendet.

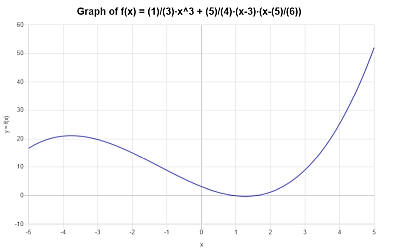
Grafisch wird das Folgende für die vereinfachte Funktion erhalten \(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\) im Intervall \([-5, 5]\):

Beispiel: verwenden eines polynomrechners

Berechnen Sie \( x^2 - (2x - 1)x \).

Lösung: In diesem letzten Beispiel haben wir \(\displaystyle x^2 - (2x - 1)x \), die wir vereinfachen müssen.

Die folgende Berechnung wird erhalten:

was die Vereinfachung beendet.

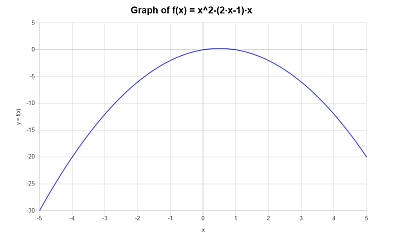
Das folgende Diagramm wird für \(\displaystyle -x^2+x\) im Intervall \([-5, 5]\) erhalten:

Weitere algebra -taschenrechner

Polynomfunktionen sind buchstäblich das Mittelstück in Algebra.Für grundlegende Anwendungen, Quadratische Polynom wird eine Schlüsselrolle und Wirtschaftlichkeit, Physik und Ingenieurwesen spielen.

Polynomfunktionen haben äußerst leistungsfähige Eigenschaften, insbesondere die Berechnung von Polynomwurzeln , die eine starke Bedeutung in Anwendungen haben.