Mehr über quadratische ungleichungen

Dieser Rechner für quadratische Ungleichungen liefert Ihnen Lösungen für Ungleichungen mit allen Schritten. Die von Ihnen angegebene Ungleichung kann zum Beispiel so etwas wie "x^2 - 1/2 > 0" sein, und im Allgemeinen sind quadratische Ungleichungen nicht allzu schwer zu lösen.

Sobald Sie eine gültige Ungleichung angeben, die quadratischer Ausdruck wenn Sie auf "Berechnen" klicken, werden Ihnen alle Schritte der Berechnung angezeigt, einschließlich eines Diagramms der Ungleichheitslösungen.

quadratische Ungleichungen sind eine der wenigen Arten (zusammen mit lineare Ungleichungen ), dass Sie garantiert eine exakte Lösung finden können, und dieser Prozess beinhaltet das Lösen einer quadratischen Gleichung.

Was ist die definition dieser art von ungleichheit?

Wir haben es nicht explizit gesagt, aber es ergibt sich schon aus dem Namen: Eine quadratische Ungleichung ist eine bestimmte Art von Ungleichung, bei der alle beteiligten Terme Polynome von höchstens Grad 2 sind. In diesem Zusammenhang ist ein Beispiel

\[\displaystyle x^2 < x - 1\]

was quadratisch ist, da beide Seiten der Ungleichung Polynome der Ordnung 2 sind. Wenn man nun:

\[\displaystyle x^2 < x^3 - 1\]

dann ist die Ungleichung nicht mehr quadratisch, weil der Term \(x^3\) auf der rechten Seite steht. Für diese Ungleichungen haben wir einen klaren Plan, um die Lösung zu finden.

Schritte zum lösen von ungleichungen, die quadratisch sind

• Schritt 1: Vergewissern Sie sich, dass es sich um eine quadratische Ungleichung handelt, da die in diesem Fall verwendete Methode nur für diese Art von Ungleichungen gilt
• Schritt 2: Wie bei den meisten Ungleichungen wird alles auf die linke Seite der Ungleichung übertragen und die zugehörige Gleichung gelöst
• Schritt 3: Wenn die zugehörige quadratische Gleichung keine reellen Wurzeln hat, dann wissen wir, dass entweder die gesamte reelle Linie eine Lösung ist oder es keine Lösung gibt. Man prüft also, ob ein beliebiger Punkt die Ungleichung löst, und wenn ja, dann ist die Lösung die gesamte reelle Linie (-∞, ∞), andernfalls ist die Lösung leer.
• Schritt 4: Wenn die zugehörige quadratische Gleichung nur eine reelle Lösung hat, bedeutet dies, dass der zugehörige quadratische Graph die x-Achse tangential berührt. Je nach Ungleichheitszeichen kann also nur der Berührungspunkt die Lösung sein, oder alles außer dem Berührungspunkt, oder die gesamte reelle Linie (-∞, ∞), für die man den Berührungspunkt und einen Punkt außerhalb davon (links und rechts vom Punkt) testen muss
• Schritt 4: Wenn die zugehörige quadratische Gleichung zwei verschiedene reelle Lösungen hat, überprüfen Sie die durch diese Wurzeln definierten Intervalle, um festzustellen, welche Teile der reellen Linie Teil der Lösung sind

Nachdem Sie die Teile analysiert haben, fügen Sie sie bei Bedarf mit dem Operator "union" zusammen, der zum Zusammenfügen von Intervallen verwendet wird.

Wie kann man eine quadratische ungleichung zeichnen?

Ungleichungen grafisch darstellen bietet eine gute Möglichkeit, die Lösung visuell darzustellen. Was das Verfahren angeht, müssen Sie wissen, ob Sie mit einer Ungleichung mit einer Variablen oder mit mehreren Variablen arbeiten.

Wenn Sie eine Ungleichheit haben wie

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

sie haben nur eine Variable, und die Lösung wird eine Teilmenge der realen Linie sein. Andererseits, wenn Sie etwas haben wie

\[\displaystyle y < x^2 - \frac{1}{2} x \]

dann gibt es nur zwei Variablen x und y, und die Lösung der Ungleichung wird eine Teilmenge der x-y-Ebene sein.

Bedeutung von quadratischen ausdrücken

Quadratische Ausdrücke, die in Gleichungen und Ungleichungen vorkommen, spielen eine grundlegende Rolle in der Mathematik. Vielleicht sind quadratische Ausdrücke nach den linearen Ausdrücken die am weitesten verbreitete Art von Strukturen.

Wenn man sich mit Kalkül und Algebra beschäftigt, findet man unzählige Anwendungen von quadratischen Ausdrücken bei Maximierungs- und Minimierungsproblemen, Integration und vielem mehr. Wenn Sie ein wenig graben, finden Sie Anwendungen von quadratischen Ausdrücken in verschiedenen wissenschaftlichen Disziplinen

Beispiel: quadratische ungleichungen

Lösen Sie diese quadratische Ungleichung: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Lösung:

Wir müssen zunächst die folgende quadratische Hilfsgleichung \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\) lösen.

Anwendung der quadratischen formel

Die quadratische Gleichung lautet:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall haben wir:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

Setzt man diese Werte in die Formel für die Wurzeln ein, erhält man:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

Also finden wir das:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Kritische punkte

Die Liste der gefundenen kritischen Punkte ist in aufsteigender Reihenfolge geordnet: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Dann müssen wir die folgenden kritischen Intervalle analysieren:

- Für das Intervall \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): Die linke Seite ist positiv, also ist \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) nicht Teil der Lösung.

- Für das Intervall \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): Die linke Seite ist negativ, was bedeutet, dass \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) ein Teil der Lösung ist.

- Für das Intervall \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) nicht Teil der Lösung ist.

Lösung

Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

In Intervallschreibweise wird die Lösung wie folgt geschrieben:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]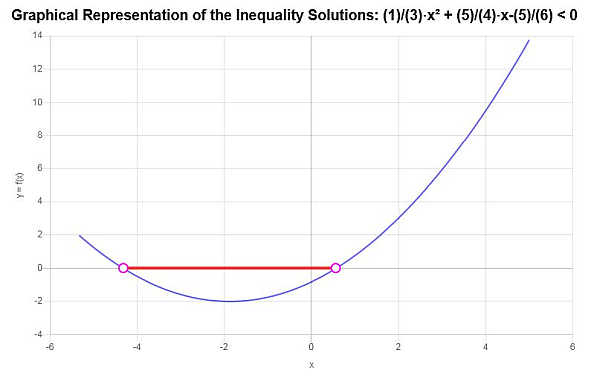

Beispiel: weitere quadratische ungleichungen

Lösen: \(x^2 < 4\)

Lösung:

Die gegebene Ungleichung lautet:

\[x^2 < 4\]

die sich zu der quadratischen Gleichung \(\displaystyle x^2-4=0\) ableitet.

Quadratische formel

Für eine quadratische Gleichung der Form \(a x^2 + bx + c = 0\) werden die Wurzeln wie folgt berechnet quadratische Formel :

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In diesem Fall ist die Gleichung, die wir lösen müssen, \(\displaystyle x^2-4 = 0\), was bedeutet, dass die entsprechenden Koeffizienten sind:

\[a = 1\] \[b = 0\] \[c = -4\]

Erstens werden wir die Diskriminanz berechnen, um die Art der Wurzeln zu bewerten.Die Diskriminierung wird berechnet als:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Da die Diskriminante in diesem Fall \(\Delta = \displaystyle 16 > 0\) ist, die positiv ist, wissen wir, dass die Gleichung zwei verschiedene reelle Wurzeln hat.

Stecken Sie diese Werte nun in die Formel für die Wurzeln, die wir erhalten:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

Also finden wir das:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

In diesem Fall hat die quadratische Gleichung \( \displaystyle x^2-4 = 0 \) zwei reelle Wurzeln, also:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

das ursprüngliche Polynom wird also als \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \) faktorisiert, womit die Faktorisierung abgeschlossen ist.

Analyse der kritischen punkte

Die Liste der gefundenen kritischen Punkte ist in aufsteigender Reihenfolge geordnet: \(-2\), \(2\).

Auf dieser Grundlage müssen wir die folgenden Intervalle analysieren:

- Für das Intervall \(\left(-\infty, -2\right)\): Die linke Seite ist positiv, also ist \(\left(-\infty, -2\right)\) nicht Teil der Lösung.

- Für das Intervall \(\left(-2, 2\right)\): Die linke Seite ist negativ, also ist \(\left(-2, 2\right)\) Teil der Lösung.

- Für das Intervall \(\left(2, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(2, \infty\right)\) nicht Teil der Lösung ist.

Lösung der ungleichheit

Ausgehend von der angegebenen Ungleichung und der Analyse der kritischen Punkte finden wir, dass die Lösung der Ungleichung lautet: \(-2< x \le 2\).

In Intervallschreibweise wird die Lösung wie folgt geschrieben:

\[\left[-2,2\right)\]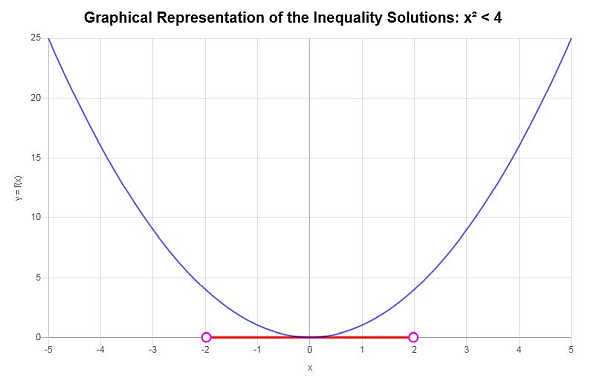

Andere nützliche ungleichheitsrechner

Die einfachste Ungleichung, die Sie lösen können, ist lineare Ungleichungen . Danach gibt es quadratische Ungleichungen, die sehr einfach sind.

Dann haben Sie polynomielle Ungleichungen diese sollten einfach zu lösen sein, aber sie können dennoch gewaltige Aufgaben darstellen, was den Umfang der zu ihrer Lösung erforderlichen Arbeit angeht.

Mit einer ungleichheitsrechner für Ungleichungen im Allgemeinen kann sich als sehr nützlich erweisen, da es sich mit den verschiedenen Arten von Ungleichungen befasst, die für die Suche nach exakten Lösungen geeignet sind.