Mehr über diesen rechner für lineare ungleichungen

Dieser Rechner gibt Ihnen die Werkzeuge an die Hand, die Sie für den Umgang mit linearen Ungleichungen benötigen. Insbesondere werden Sie in der Lage sein, sie zu lösen und grafisch darzustellen, indem Sie alle Schritte gezeigt bekommen.

Lineare Ungleichungen wie "2x + 3 < 1" oder "3x + 2y <=1" sind zulässig, und je nach Anzahl der Variablen erhalten Sie einen passenden Graphen mit den Schritten, die zur Lösung führen.

Sobald Sie eine gültige lineare Ungleichung eingegeben haben, müssen Sie nur noch auf "Lösen" klicken, um den Prozess zu starten. Wenn etwas falsch ist oder fehlt, wird der Rechner Sie darauf hinweisen.

Diese Art von Ungleichungen ist die einfachste Art, die Sie finden werden, und sie sind immer relativ leicht zu lösen. Diese Art zusammen mit quadratische Ungleichungen gehören zu den einzigen "leicht" zu lösenden Ungleichungen.

Was ist eine lineare ungleichung?

Eine lineare Ungleichung ist die einfachste Art der Ungleichung, bei der alle beteiligten Terme linear oder konstant sind.

\[\displaystyle a x + b y \le 1\]

Die obige Gleichung ist zum Beispiel eine lineare Gleichung mit zwei Variablen. Technisch gesehen, haben wir polynomiale Ungleichung vom Grad 1, aber das ist eine etwas zu komplizierte Sichtweise.

Wie löst man eine lineare ungleichung?

• Schritt 1: Legen Sie alles, was die zu lösende Variable enthält, auf die eine Seite und den Rest auf die andere Seite
• Schritt 2: Gruppe und vereinfachen Sie den Ausdruck so zu reduzieren wie die Begriffe
• Schritt 3: Wenn eine Konstante ungleich eins die Variable multipliziert, für die Sie eine Lösung finden wollen, dividieren Sie durch sie. Eine Einschränkung: Wenn Sie durch einen negativen Wert dividieren, müssen Sie die Richtung der Ungleichung ändern

Einer der wichtigsten Punkte, den es zu beachten gilt und der die Prozesse des Lösens von Gleichungen und Ungleichungen unterscheidet, ist, dass wir beim Lösen von Gleichungen freier mit Konstanten multiplizieren (oder dividieren) können und sich nichts ändert, während wir bei Ungleichungen vorsichtiger sein müssen, da das Multiplizieren (oder Dividieren) mit negativen Konstanten die Richtung der Ungleichung ändert.

Was ist die allgemeinste lineare ungleichung?

Das allgemeinste, was man mit linear erreichen kann, ist

\[\displaystyle a x + bx \le c\]

aber dennoch kann es sein, dass Sie '<' anstelle von '\(\le\)' haben. Oder wir könnten haben

\[\displaystyle a x + bx \ge c\]

aber Sie könnten auch '>' anstelle von '\(\ge\)' verwenden.

Ähnlich wie bei Addition und Subtraktion wird die Trennung von Fraktionen nur aus der Multiplikation von Fraktionen abgeleitet: Um zwei Brüche zu teilen, multiplizieren Sie sich nur zuerst mit dem umgekehrter Bruch des zweiten (die inverse Fraktion wird durch Tausch des Zählers durch den Nenner in der Fraktion erhalten).

Anwendungen

Lineare Ungleichungen finden in der Mathematik eine Vielzahl von Anwendungen. Eine lineare Ungleichung ist eine Art gewichteter Durchschnitt, der sich sehr gut für alle Arten von Misch- und Zuordnungsproblemen eignet.

Bei der Bearbeitung von Textaufgaben stößt man in der Regel auf lineare Gleichungen, aber es ist nicht ungewöhnlich, dass man auch mit linearen Ungleichungen konfrontiert wird.

Eines der bekanntesten Gebiete ist die Optimierung und lineare Programmierung, bei der lineare Ungleichungen eine entscheidende Rolle spielen, sowohl mit der Simplex-Methode als auch mit den Kuhn-Tucker-Bedingungen, wenn es um eine nichtlineare Zielfunktion geht.

Beispiel: lösen von ungleichungen

Lösen Sie die folgende lineare Ungleichung: \(\frac{2}{3} x + \frac{5}{4} < - \frac{1}{6}\)

Lösung:

Wir müssen alle Begriffe der Ungleichheit auf eine Seite stellen:

\[\frac{2}{3}x+\frac{5}{4}- \left(-\frac{1}{6}\right)< 0\]

Zugehörige hilfsgleichung

Wir müssen eine Lösung finden:

\[\frac{2}{3}x+\frac{5}{4}-\left(-\frac{1}{6}\right)=0\]

Schritt 0: In diesem Fall müssen wir zunächst die gegebene lineare Gleichung vereinfachen, und dazu führen wir die folgenden Vereinfachungsschritte durch:

Lösen der linearen gleichung

Setzt man \(x\) auf die linke Seite und die Konstante auf die rechte Seite, erhält man

\[\displaystyle \frac{2}{3}x = -\frac{17}{12}\]

Löst man nun \(x\), indem man beide Seiten der Gleichung durch \(\frac{2}{3}\) dividiert, erhält man folgendes

\[\displaystyle x = \displaystyle \frac{ -\frac{17}{12}}{ \frac{2}{3}}\]

und vereinfachen wir endlich die folgenden

\[\displaystyle x=-\frac{17}{8}\]

Daher führt die Lösung von \(x\) für die gegebene lineare Gleichung zu \(x=-\frac{17}{8}\).

Kritische punkte

Wie bei einer linearen Ungleichung zu erwarten, gibt es nur einen kritischen Punkt, nämlich \(-\frac{17}{8}\), von dem aus wir die folgenden Intervalle analysieren:

- Für das Intervall \(\left(-\infty, -\frac{17}{8}\right)\): Die linke Seite ist negativ, was bedeutet, dass \(\left(-\infty, -\frac{17}{8}\right)\) Teil der Lösung ist.

- Für das Intervall \(\left(-\frac{17}{8}, \infty\right)\): Die linke Seite ist positiv, was bedeutet, dass \(\left(-\frac{17}{8}, \infty\right)\) nicht Teil der Lösung ist.

Lösung der ungleichheit

Daraus ergibt sich, dass die Lösung der Ungleichung lautet: \(x < -\frac{17}{8}\).

Der Ausdruck der Lösung mit Intervallnotation, die Lösung wird geschrieben als:

\[\left(-\infty,-\frac{17}{8}\right)\]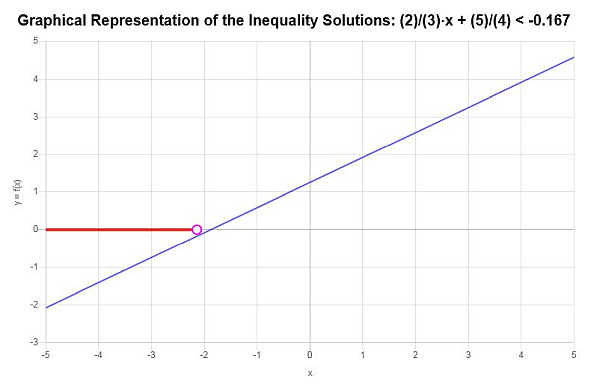

Beispiel: weitere lineare ungleichungen

Lösen Sie diese lineare 2-Variablen-Ungleichung: \(\frac{1}{3} x + \frac{5}{4} y < - \frac{5}{6}\)

Lösung:

Wir müssen eine Lösung finden:

\[\frac{1}{3}x+\frac{5}{4}y < -\frac{5}{6}\]

Wir haben eine lineare Ungleichung gegeben, und wir müssen für die Variable \(y\) lösen.

In diesem Fall lösen wir \(y\), also setzen wir es auf die eine Seite der Ungleichung und den Rest auf die andere Seite und erhalten:

\[\frac{5}{4}y<-\frac{1}{3}x-\frac{5}{6}\]

Um \(y\) zu lösen, dividieren wir beide Seiten der Ungleichung durch \(\frac{5}{4}\), so dass wir schließlich erhalten:

\[y < -\frac{4}{15}x-\frac{2}{3}\]

Lösung einer linearen ungleichung

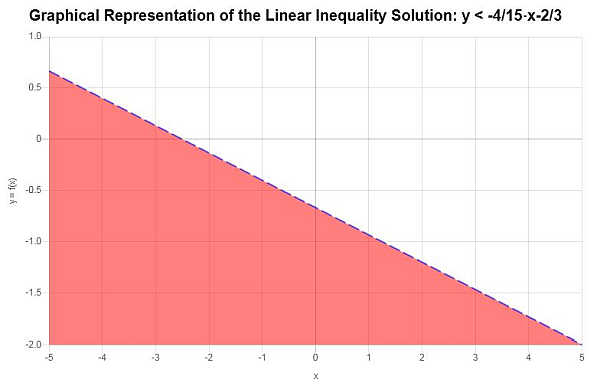
Ausgehend von der angegebenen Ungleichung erhalten wir nach Lösung für \(y\):

\[y < -\frac{4}{15}x-\frac{2}{3}\]

Die grafische Darstellung des Lösungsbereichs ist in der nachstehenden Grafik zu sehen:

Weitere algebra -taschenrechner

Der Umgang mit dem Ausdruck ist in der Algebra entscheidend. Vereinfachung des Ausdrucks steht am Anfang der meisten mathematischen Prozesse, und man muss die Dinge in der Regel auf ihren einfachsten Ausdruck reduzieren.

Lösen von Gleichungen und auch Lösen von Ungleichungen wird bei den meisten Prozessen im Mittelpunkt stehen, da das eine oder das andere bei fast allem, was Sie in Mathematik tun, im Mittelpunkt stehen wird.