Mehr über den cross product calculator

Mit diesem Taschenrechner können Sie das berechnen kreuzprodukt zweier Vektoren . Alles, was Sie tun müssen, ist, die beiden Vektoren anzugeben, für die Sie die kreuzprodukt .

Das Kreuzprodukt ist eine Operation, die für zwei dreidimensionale Vektoren \(x = (x_1,x_2,x_3)\) und \(y = (y_1, y_2, y_3)\) durchgeführt wird, und das Ergebnis der Operation ist ein dreidimensionaler Vektor.

Produktübergreifende formel

Die Berechnung des Kreuzprodukts ist nicht allzu kompliziert und hat eine gute Gedächtnisstütze. Die Formel für das Kreuzprodukt ist unten dargestellt:

#XYZA

Diese Formel, ausgedrückt als 3x3-Determinante, ist vielleicht die am leichtesten zu merkende Formel. Die Formeln, die sich speziell auf die Komponenten \(x_{ij}\) und \(y_{ij}\) beziehen, sind viel schwieriger zu merken.

Dies könnte für ein Kreuzprodukt in 4d verallgemeinert werden, aber das sprengt den Rahmen dieses Rechners, in dem wir uns nur mit 3d-Berechnungen beschäftigen.

Produktübergreifende interpretation

Das Kreuzprodukt hat eine starke geometrische Motivation. Zunächst einmal ist das Kreuzprodukt ein Vektorprodukt, d. h. man gibt zwei Vektoren vor, und das Ergebnis ist ein weiterer Vektor.

In der Tat entspricht das Kreuzprodukt einem Vektor mit größenordnung ist gleich der Fläche des Parallelogramms, das durch die Vektoren \(x\) und \(y\) gebildet wird.

Außerdem hat der resultierende Vektor eine Richtung, die senkrecht auf die Ebene, die durch die Vektoren \(x\) und \(y\) gebildet wird.

Das Kreuzprodukt hat also in der Tat eine dreidimensionale Darstellung, und zwar zunächst durch das Parallelogramm, das durch die beiden Vektoren ausgedrückt wird, und den dazu senkrecht stehenden Vektor.

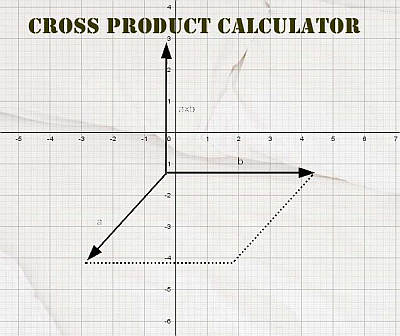
Das kreuzprodukt und das punktprodukt

Eine verwandte Operation für zwei Vektoren ist die punktprodukt allerdings ist das Ergebnis eines Punktprodukts ein Skalar und kein Vektor. Das Kreuzprodukt und das Punktprodukt sind in vielerlei Hinsicht verwandt, werden aber in unterschiedlichen Zusammenhängen verwendet.

Abgesehen davon vektor-Kreuzprodukt-Rechner haben Sie ein Skalarprodukt, das durch den punktprodukt .